Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi chiều dài mảnh vườn là a(m)
Khi đó ta có \(2a + 2x = 40 \Leftrightarrow a = 20 - x\)
Vậy diện tích mảnh vườn hình chữ nhật là: \(S = a.x = (20 - x)x = - {x^2} + 20x\)
b) Để diện tích mảnh vườn lớn nhất thì S phải lớn nhất:
Ta có \(S = - {x^2} + 20x = - ({x^2} - 20x + 100) + 100 = 100 - {(x - 10)^2} \le 100\)(vì \({(x - 10)^2} \ge 0\))
Diện tích mảnh vườn lớn nhất là 100 \(\left( {{m^2}} \right)\) khi x = 10

Gọi x là chiều rộng của vườn hoa (\(x > 0\), tính bằng đơn vị mét)
Theo giả thiết ta có chiều dài là \(15 - x\)
Diện tích của vườn hoa có phương trình như sau \(f\left( x \right) = x\left( {15 - x} \right) = - {x^2} + 15x\)
Ta có bất phương trình thỏa mãn bài toán như sau:\( - {x^2} + 15x \ge 50 \Leftrightarrow - {x^2} + 15x - 50 \ge 0\)
Xét tam thức \(g\left( x \right) = - {x^2} + 15x - 50\) có hai nghiệm phân biệt là \({x_1} = 5;{x_2} = 10\) và \(a = - 1 < 0\) nên \(g\left( x \right) > 0\) khi x thuộc đoạn \(\left[ {5;10} \right]\)
Vậy khi chiều rộng nằm trong đoạn \(\left[ {5;10} \right]\) mét thì diện tích vườn hoa ít nhất là 50 \({m^2}\).

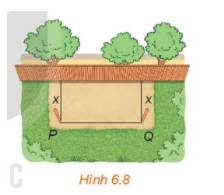
a) Theo bài ra ta có: \(x + x + PQ = 20 \Rightarrow PQ = 20 - 2x\)(m)
b) Diện tích của mảnh đất được rào chắn là: \(\)\(x.PQ = x.(20 - 2x) = - 2{x^2} + 20x({m^2})\)

Để diện tích của mảnh vườn không nhỏ hơn 48 \({m^2}\)thì
\(S(x) \ge 48 \Rightarrow - 2{x^2} + 20x \ge 48 \Leftrightarrow - 2{x^2} + 20x - 48 \ge 0\)

Diện tích mỗi phần:
\(\left(\frac{15}{4}\cdot\frac{2}{3}\right):5=\frac{1}{2}\left(m^2\right)\)
Đáp số : \(\frac{1}{2}m^2\)

Giả sử người ta có thể rào đủ mảnh vườn
Gọi hai cạnh mảnh vườn có độ dài lần lượt là x,y với x,y >0
\(\Rightarrow2x+y=100\)
\(100=2x+y\ge2\sqrt{2xy}\Rightarrow\sqrt{2xy}\le50\)
\(\Rightarrow2xy\le2500\Rightarrow xy\le1250\)
\(S_{max}=1250\left(m^2\right)\) khi \(\left\{{}\begin{matrix}2x+y=100\\2x=y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=25\\y=50\end{matrix}\right.\)

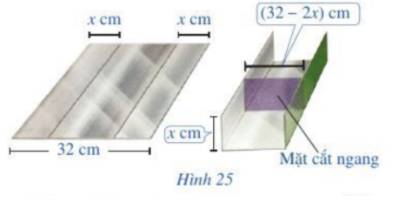
Mặt cắt ngang là hình chữ nhật với chiều dài là 32 - 2x và chiều rộng là x (cm).
Diện tích mặt cắt là: \(x.(32-2x)\)
Để đảm bảo yêu cầu kĩ thuật thì :\(x.(32 - 2x) \ge 120 \)\(\Leftrightarrow 2{x^2} - 32x + 120 \le 0\)
Tam thức bậc hai \(2{x^2} - 32x + 120\) có hai nghiệm là \({x_1} = 6;{x_2} = 10\) và có hệ số \(a=2>0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho tam thức \(2{x^2} - 32x + 120\) mang dấu "-" là \(\left( { 6;10} \right) \)
Tức là rãnh nước phải có độ cao lớn hơn 6cm và nhỏ hơn 10cm.