Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A
Hướng dẫn:
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A

Lấy ba điểm A, B, C phân biệt trên đường viền.
Dựng đường trung trực của AB và BC. Hai đường trung trực này cắt nhau tại O.
Khi đó; OA = OB = OC
Suy ra: O là tâm của đường viền.

Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A

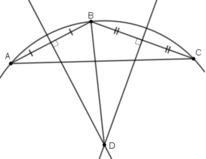
Để xác định được bán kính ta cần xác định được tâm của đường tròn chứa chi tiết máy này. Ta xác định tâm như sau:
+ Lấy ba điểm phân biệt A, B, C trên đường viền ngoài chi tiết máy.
+ Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại D. Khi đó D là tâm cần xác định.
+ Bán kính đường tròn cần tìm là độ dài đoạn DB (hoặc DA hoặc DC).
Ta có hình vẽ minh họa

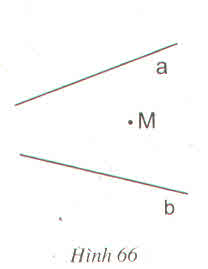
- Vẽ đường thẳng qua M vuông góc với a tại P cắt b tại Q.
- Vẽ đường thẳng qua M vuông góc với b tại R cắt a tại S.
- Vẽ đường thẳng qua M vuông góc với SQ.
=> Đây chính là đường qua M và qua giao điểm của hai đường a, b.

Áp dụng bài 69 ta có cách vẽ sau:
-Vẽ đường thẳng qua M vuông góc với a tại A cắt b tại B.
-Vẽ đường thẳng qua M vuông góc với b tại C cắt a tại D.
-Vẽ đường thẳng c qua M vuông góc với BD
=>C là đường qua M và qua giao điểm của hai đường a, b
Vì 3 đường thẳng a, b, c là 3 đường cao trong ∆DMB nên đồng quy

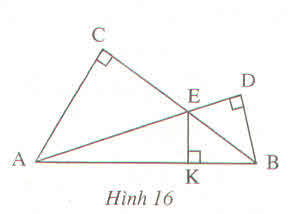
Xét ΔAEB có
AC là đường cao
BD là đường cao
EK là đường cao
Do đó: AC,BD,EK cùng đi qua một điểm

a) Ta có điểm A có tọa độ xA = 2, yA = 1
Vì điểm A thuộc đồ thị hàm số y = ax nên ta có:
1 = a.2 => a = \(\dfrac{1}{2}\)
Vậy hệ số a bằng \(\dfrac{1}{2}\), ta có hàm số y = \(\dfrac{1}{2}x\)
b) Lúc này đường thẳng OA là đồ thị của hàm số y = \(\dfrac{1}{2}x\)
Khi x = \(\dfrac{1}{2}\) thì y = \(\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{4}\)
Ta có điểm B trên đồ thị có tọa độ B(\(\dfrac{1}{2};\dfrac{1}{4}\))
c) Thay y = -1 vào hàm số y = \(\dfrac{1}{2}x\), ta có:
-1 = \(\dfrac{1}{2}x\) => x = -2
Khi đó điểm C trên đồ thị có tọa độ C(-2; -1)
a) Vì A(2;1) thuộc đồ thị của hàm số y= ax nên thay x = 2 ; y = 1 vào công thức y=ax . Ta có :

b) Từ điểm 1/2= a.2 ⇒ a =1/2
trên trục hoành vẽ đường thẳng song song trục tung cắt đồ thị tại điểm B. B là điểm cần đánh dấu. c) Từ điểm -1 trên trục tung vẽ đường thẳng song song với trục hoành cắt đồ thị tại điểm C. C là điểm cần đánh dấu.
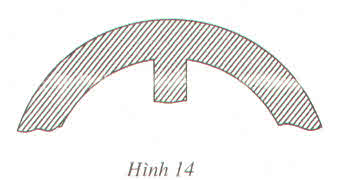
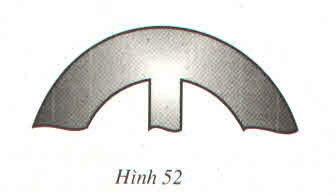
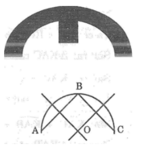






- Lấy 3 điểm A, B, C bất kì trên đường viền. Ba điểm này tạo thành tam giác ABC và tâm và bán kính đường tròn ngoại tiếp tam giác này chính là tâm và bán kính của đường viền.
- Vẽ trung trực của 2 cạnh AB, BC, chúng cắt nhau tại O. Từ tính chất đường trung trực suy ra OA = OB = OC
Do đó O chính là tâm đường tròn này. Khi đó OA hoặc OB hoặc OC chính là bán kính cần xác định.