Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giả sử tam giác ABC có 2 đường trung tuyến BM và CN gặp nhau ở G
=> G là trong tâm của tam giác
-> GB=BM ; GC = CN
mà BM=CN (gt) nên GB = GC
=> tam giác GBC cân tại G
Do đó tam giác BCN=tam giác CBM vì:
BC là cạnh chung
CN = BM (gt)
=> tam giác ABC cân tại A
xét tam giác ABD và ACE :
E=D (=90o)
CE=BD (gt)
A:chung
suy ra tam giác ABD =ACE(ch_gn)
suy ra góc B=C(t/ư)
xét tam giác EIB&DIC:
E=D(=90o)
IE=ID
B=C
suy ra tam giácEIB=DIC
suy ra IB=IC
suy ra tam giác BIC cân tại I, suy ra B=C
suy ra:đpcm
Hãy chứng minh định lý đảo sau: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Gọi Δ ABC có trung tuyến BM = CN, G là trọng tâm Δ (giao điểm các trung tuyến)
Ta có :
GB = 2/3.BM
GC = 2/3.CN
Mà BM = CN => GB = GC
=> Δ BGC cân tại G
=> ∠ MBC = ∠ NCB
Xét Δ BMC và Δ CNB :
BM = CN
∠ MBC = ∠ NCB
BC là cạnh chung
=> Δ BMC = Δ CNB (c - g - c)
=> ∠ MCB = ∠ NBC
hay ∠ ACB = ∠ ABC
=> Δ ABC cân tại A (đpcm)
k nha

Giả sử ∆ABC có hai đường trung tuyến BM và CN gặp nhau ở G => G là trọng tâm của tam giác => GB = BM; GC = CN mà BM = CN (giả thiết) nên GB = GC => ∆GBC cân tại G => do đó ∆BCN = ∆CBM vì: BC là cạnh chung CN = BM (gt) (cmt) => => ∆ABC cân tại A

định lí đảo của định lí trên là: trong 1 tam giác cân thì 2 đường trung tuyến nối từ 2 đỉnh ở đáy bằng nhau
giả sử ta có tam giác ABC cân tại A, BD là đường trung tuyến nối từ đỉnh B tới AC( D thuộc AC); CE là đường trung tuyến nối từ đỉnh C tới AB( E thuộc AB)
suy ra B=C và
AC=AB suy ra 1/2 AB=1/2AC suy ra EA=EB=DE=DC
xét tam giác DBC và tam giác ECB có:
EB=DC(cmt)
BC(chung)
B=C(tam giác ABC cân tại A)
suy ra tam giac sDBC=ACB(c.g.c)
suy ra EC=BD

giả sử đó là tam giác abc, am là trugn tuyến của tam giác abc =>mb=mc
vì am là đg phân giác => góc mab = góc mac
Xét tam giác amb và tam giác amc có:
góc mab = góc mac(cmt)
mb=mc (cmt)
am chung
=> tam giác amb= tam giác amc(c.g.c)
=> <mab=<mac( hia cạnh tg ứng)
xét tam giác abc có <b=<c (chứng minh trên)
= tam giác abc cân

Giả sử ∆ABC có hai đường trung tuyến BM và CN gặp nhau ở G
=> G là trọng tâm của tam giác
=> GB = BM; GC = CN
mà BM = CN (giả thiết) nên GB = GC
=> ∆GBC cân tại G => ˆGCB=ˆGBCGCB^=GBC^
do đó ∆BCN = ∆CBM vì:
BC là cạnh chung
CN = BM (gt)
ˆGCB=ˆGBCGCB^=GBC^ (cmt)
=> ˆNBC=ˆMCBNBC^=MCB^ => ∆ABC cân tại A

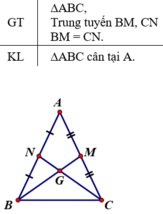
Giả sử ΔABC có hai đường trung tuyến BM và CN cắt nhau tại G.
⇒ G là trọng tâm của tam giác
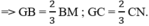
Mà BM = CN (theo gt) ⇒ GB = GC ⇒ GM = GN.
Xét ΔGNB và ΔGMC có :
GN = GM (cmt)
GB = GC (cmt)
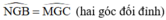
⇒ ΔGNB = ΔGMC (c.g.c) ⇒ NB = MC.
Lại có AB = 2.BN, AC = 2.CM (do M, N là trung điểm AC, AB)
⇒ AB = AC ⇒ ΔABC cân tại A.