Chứng minh các phân thức sau luôn xác định với mọi x 2 x +...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

17 tháng 2 2018

Chứng minh các phân thức sau luôn xác định với mọi x

2 x + 3 8 x - 18 - x 2

#Toán lớp 8

Cao Minh Tâm

17 tháng 2 2018

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Pham Trong Bach

24 tháng 5 2017

Chứng minh các phân thức sau luôn xác định với mọi x

x 2 + 2 x + 3 - 12 + 6 x - x 2

#Toán lớp 8

Cao Minh Tâm

24 tháng 5 2017

Đúng(0)

Huỳnh Hoàng Châu

6 tháng 7 2016 - olm

1/ Chứng minh đa thức sau luôn dương với mọi x:

x²- x + 1

2/ Chứng minh các đa thức sau luôn âm với mọi x:

a) (x - 3)(1 - x) - 2

b) (x + 4)(2 - x) - 10

#Toán lớp 8

Hoàng Phúc

6 tháng 7 2016

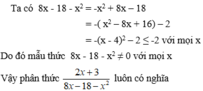
\(1,x^2-x+1=x^2-2.x.\frac{1}{2}+\left(\frac{1}{2}\right)^2+\frac{3}{4}=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\)

Vì \(\left(x-\frac{1}{2}\right)^2\ge0=>\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\) (với mọi x)

Vậy ........

\(2,a,\left(x-3\right)\left(1-x\right)-2=x-x^2-3+3x-2=-x^2+4x-5=-\left(x^2-4x+5\right)\)

\(=-\left(x^2-4x+4+1\right)=-\left(x^2-2.x.2+2^2+1\right)=-\left[\left(x-2\right)^2+1\right]=-1-\left(x-2\right)^2\)

Vì \(\left(x-2\right)^2\ge0=>-\left(x-2\right)^2\le0=>-1-\left(x-2\right)^2\le-1< 0\) (với mọi x)

Vậy........

\(b,\left(x+4\right)\left(2-x\right)-10=2x-x^2+8-4x-10=-x^2-2x-2=-\left(x^2+2x+2\right)=-\left(x^2+2x+1+1\right)\)

\(=-\left(x^2+2.x.1+1^2+1\right)=-\left(x+1\right)^2+1=-1-\left(x+1\right)^2\le-1< 0\) (với mọi x)

Vậy.......

Đúng(0)

Thắng Tran Duc

23 tháng 9 2016

1. chứng minh các biểu thức sau luôn lớn hơn 0 với mọi x

a, A=x-3x+5

b,B=2x-8x+18

c,C=(x-1)²-2*(x+2)*(x-1)+3*(x+2)²

d,D=x²-2xy+3y²-4y+8

#Toán lớp 8

Chan Nước Mắm Cơm

23 tháng 9 2016

Hình như bạn viết sai đề,câu a câu b có x^2 mới đúng chứ?

Đúng(0)

Thắng Tran Duc

23 tháng 9 2016 - olm

1. chứng minh các biểu thức sau luôn lớn hơn 0 với mọi x

a, A=x-3x+5

b,B=2x-8x+18

c,C=(x-1)²-2*(x+2)*(x-1)+3*(x+2)²

d,D=x²-2xy+3y²-4y+8

#Toán lớp 8

Nguyễn Thanh Hằng

19 tháng 8 2020 - olm

chứng minh rằng các biểu thức sau luôn luôn dương với mọi x

A = x (x - 6) + 10

B = x² - 2x + 9y² - 6y + 3

#Toán lớp 8

Nguyễn Việt Hoàng

19 tháng 8 2020

+) \(A=x\left(x-6\right)+10\)

\(A=x^2-6x+10\)

\(A=x^2-6x+9+1\)

\(A=\left(x-3\right)^2+1\ge1\)

Vậy.....

+) \(B=x^2-2x+9y^2-6y+3\)

\(B=\left(x^2-2x+1\right)+\left(9y^2-6y+1\right)+1\)

\(B=\left(x-1\right)^2+\left(3y-1\right)^2+1\ge1\)

Vậy .....

Đúng(0)

Nguyễn Thanh Hằng

19 tháng 8 2020

thanks bạn nhìu

Đúng(0)

Phan Thị Thương

9 tháng 12 2018 - olm

Cho phân thức \(\frac{3x^3+6x^2}{x^3+x^2+x+2}\)

a) Tìm điều kiện của x để giá trị của phân thức được xác định

b) Chứng tỏ rằng giá trị của phân thức luôn luôn không âm khi nó được xác định

#Toán lớp 8

Yến Nguyễn

28 tháng 6 2016 - olm

chứng minh các biểu thức sau luôn âm với mọi giá trị của x

-x^2-1

-(x+1)^2

-(x+1)^2-3

#Toán lớp 8

Oo Bản tình ca ác quỷ oO

28 tháng 6 2016

chứng minh nó luôn bé hơn 0!!!

675675867876896978987985685686586

Đúng(0)

Hoàng Tuấn Nam

28 tháng 6 2016

a)-x² -1=-(x²+1)

Vì x² >= 0 nên x² +1>0 nên -(x²+1)<0 hay -x² -1<0

b)Vì (x+1)² >=0 nên -(x+1)² <=0. Phần này biểu thức bằng 0 với giá trị x=1 chứ không thể luôn âm được.

c)Theo b) -(x+1) <=0 nên -(x+1)² -3<0

Đúng(0)

Yến Nguyễn

27 tháng 6 2016

chứng minh các biểu thưc sau luôn dương với mọi giá trị của x

x^2-x+1

x^2+5x+8

3x^2+6x+3

#Toán lớp 8

Lê Chí Công

27 tháng 6 2016

x^2-x+1/4+3/4

=[x-1/2]^2+3/4>0

Vay....

2 câu kia tương tự nha

Đúng(0)

Ngô Trần Hải Quỳnh

17 tháng 8 2016 - olm

Chứng minh các biểu thức sau đây luôn luôn dương với mọi x , y

A=(x - 3)(x -5) + 2

B = x² - 5x + 7

C = x²- xy + y²

#Toán lớp 8

Nguyễn Trần Sỹ An

17 tháng 8 2016

A=(x-3)(x-5)+2=x^2-5x-3x+15+2=x^2-8x+17=x^2-8x+16+1=(x-4)^2+1>0

B=x^2-5x+7=x^2-5/2*2x+(5/2)^2-(5/2)^2+7=(x-5/2)^2+3/4>0

C=x^2-xy+y^2=x^2-1/2*2xy+1/4y^2-1/4y^2+y^2=(x-1/2y)^2+3/4y^2>0

Đúng(0)

Lyzimi

17 tháng 8 2016

A=(x-3)(x-5)+2

=x²-8x+15+2

=x²-8x+16+1

=(x-4)²+1

vì (x-4)² lớn hơn hoặc = 0 nên (x-4)²+1 dương

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP