Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng tính chất tia phân giác, ta có \(\dfrac{ED}{EC}=\dfrac{AD}{AC}\) và \(\dfrac{ED}{EC}=\dfrac{BD}{BC}\). Từ đó suy ra \(\dfrac{AD}{AC}=\dfrac{BD}{BC}\Rightarrow AD.BC=AC.BD\) (đpcm)

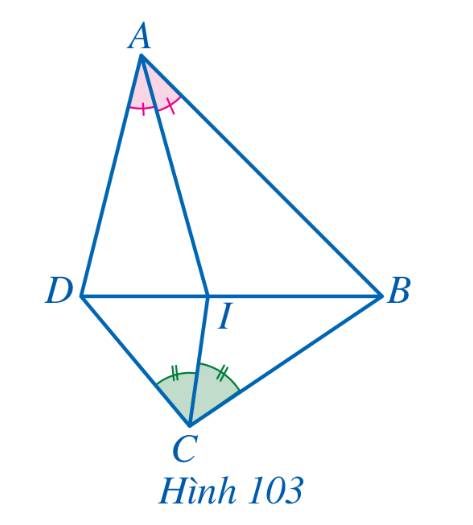
Vì AI là đường phân giác của góc DAB nên \(\frac{{ID}}{{IB}} = \frac{{AD}}{{AB}}\) (Tính chất đường phân giác)
Vì CI là đường phân giác của góc BCD nên \(\frac{{ID}}{{IB}} = \frac{{CD}}{{CB}}\) (Tính chất đường phân giác)
\( \Rightarrow \frac{{AD}}{{AB}} = \frac{{CD}}{{CB}} \Rightarrow AB.CD = AD.BC\)

Gọi giao điểm hai đường chéo của hình thoi là O.
Khi đó AC vuông góc với BD tại O.
Vì ABCD là hình thoi nên \(AB = AD\) hay tam giác ABD cân tại A.
Khi đó AO vừa là đường cao, vừa là phân giác của tam giác ABD.
Xét tam giác AMD với AN là đường phân giác, ta có:
\(\frac{{ND}}{{NM}} = \frac{{AD}}{{AM}}\,\,\left( 1 \right)\) (Tính chất đường phân giác)
Mà \(AB = 3AM \Rightarrow \frac{{AB}}{{AM}} = 3 \Rightarrow \frac{{AD}}{{AM}} = 3\,\,\left( 2 \right)\)
Từ (1) và (2) ta có: \(\frac{{ND}}{{NM}} = 3 \Rightarrow ND = 3NM\).

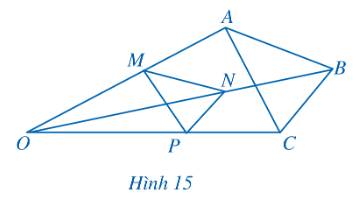
Xét tam giác OAB có \(\frac{{OM}}{{MA}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Xét tam giác OBC có \(\frac{{OP}}{{PC}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Từ đó ta có \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}}\).
Xét tam giác OAC với \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}} \Rightarrow MP\parallel AC\) (Hệ quả của định lý Thales).

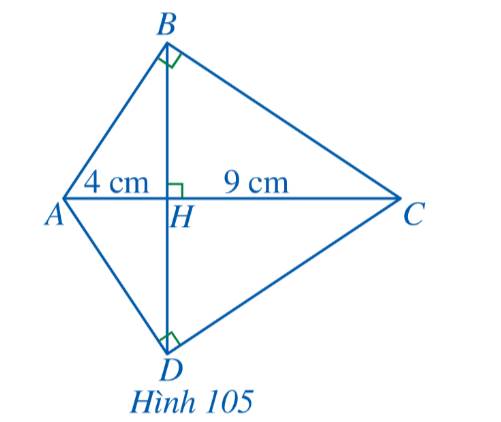
a) Xét tam giác ABC vuông tại B có: \(\widehat {BAC} + \widehat {BCA} = 90^\circ \)
Xét tam giác BHC vuông tại H có:
\(\begin{array}{l}\widehat {HBC} + \widehat {HCB} = 90^\circ \\ \Rightarrow \widehat {HBC} + \widehat {BCA} = 90^\circ \end{array}\)
\( \Rightarrow \widehat {HBC} = \widehat {BAC}\) hay \(\widehat {HBC} = \widehat {BAH}\)
Xét tam giác HAB và tam giác HBC có:
\(\widehat {BAH} = \widehat {CBH}\) và \(\widehat {BHA} = \widehat {CHB} = 90^\circ \)
\( \Rightarrow \Delta HAB \backsim \Delta HBC\)
b) Vì \(\Delta HAB \backsim \Delta HBC\) nên
\(\begin{array}{l}\frac{{HA}}{{HB}} = \frac{{HB}}{{HC}}\\ \Rightarrow H{B^2} = HA.HC\\ \Rightarrow H{B^2} = 4.9 = 36\\ \Rightarrow HB = 6cm\end{array}\)
Ta chứng minh được \(\Delta HAD \backsim \Delta HDC\)
\(\begin{array}{l} \Rightarrow \frac{{HA}}{{HD}} = \frac{{HD}}{{HC}}\\ \Rightarrow H{D^2} = HA.HC\\ \Rightarrow H{D^2} = 4.9 = 36\\ \Rightarrow HD = 6cm\end{array}\)
Vậy \(HB = HD = 6cm\).

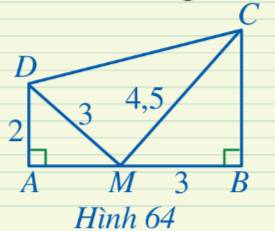
Vì \(\frac{{AD}}{{BM}} = \frac{2}{3},\,\,\frac{{DM}}{{MC}} = \frac{3}{{4,5}} = \frac{2}{3}\) nên \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\).
Xét hai tam giác \(ADM\) và \(BMC\) có \(\widehat {MAD} = \widehat {CBM} = 90^\circ \) và \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\) nên \(\Delta{ADM} \backsim \Delta{BMC}\).
Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\).
Xét tam giác \(ADM\) vuông tại A có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\widehat {AMD} + \widehat {ADM} = 90^\circ \\ \Rightarrow \widehat {AMD} + \widehat {BMC} = 90^\circ \end{array}\)
Mà ta có:
\(\begin{array}{l}\,\,\,\,\,\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = 180^\circ \\ \Rightarrow 90^\circ + \widehat {DMC} = 180^\circ \\ \Rightarrow \widehat {DMC} = 90^\circ \end{array}\)
Vậy tam giác \(CDM\) vuông tại \(M\).

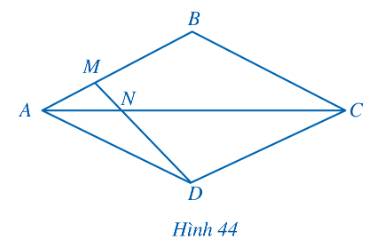
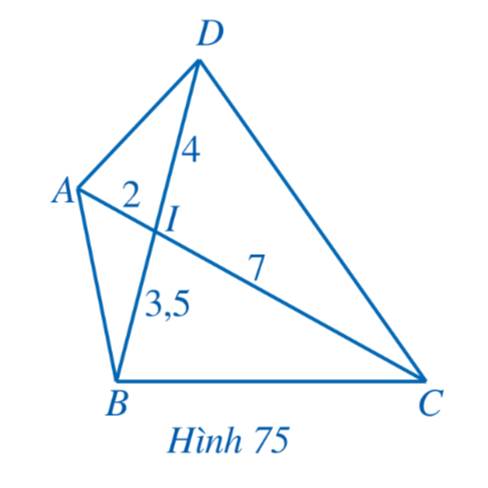
a) Ta thấy \(\frac{{IA}}{{ID}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{IB}}{{IC}} = \frac{3}{6} = \frac{1}{2}\)
\( \Rightarrow \frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\)
Mà \(\widehat {AIB} = \widehat {DIC}\) (hai góc đối đỉnh)
Xét tam giác IAB và tam giác IDC có:
\(\frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\) và \(\widehat {AIB} = \widehat {DIC}\)
\( \Rightarrow \)\(\Delta IAB \backsim \Delta IDC\) (c-g-c)
b) Ta thấy \(\frac{{IA}}{{IB}} = \frac{2}{3};\,\,\frac{{ID}}{{IC}} = \frac{4}{6} = \frac{2}{3}\)
\( \Rightarrow \frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\)
Mà \(\widehat {AID} = \widehat {BIC}\) (hai góc đối đỉnh)
Xét tam giác IAD và tam giác IBC có:
\(\frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\) và \(\widehat {AID} = \widehat {BIC}\)
\( \Rightarrow \)\(\Delta IAD \backsim \Delta IBC\) (c-g-c)

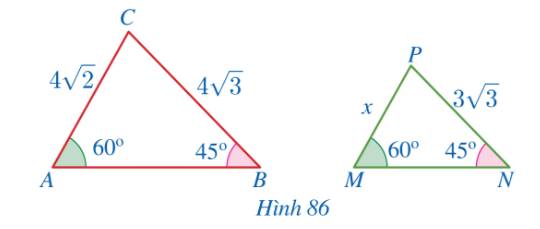
a) Xét tam giác ABC và tam giác MNP có:
\(\begin{array}{l}\widehat A = \widehat M = 60^\circ \\\widehat B = \widehat N = 45^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g)
b) Vì \(\Delta MNP \backsim \Delta ABC\) nên \(\frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) (Tỉ số đồng dạng)
\(\begin{array}{l} \Rightarrow \frac{{4\sqrt 2 }}{x} = \frac{{4\sqrt 3 }}{{3\sqrt 3 }}\\ \Rightarrow x = \frac{{4\sqrt 2 .3\sqrt 3 }}{{4\sqrt 3 }} = 3\sqrt 2 \end{array}\)
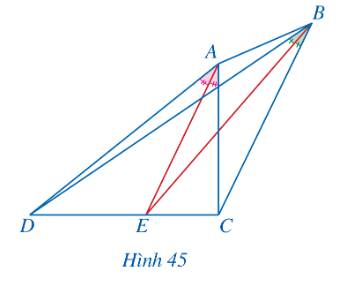
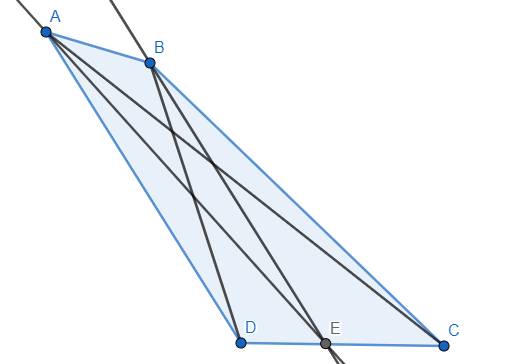
Xét tam giác ACD với đường phân giác AE, ta có:
\(\frac{{ED}}{{EC}} = \frac{{AD}}{{AC}}\,\,\left( 1 \right)\) (Tính chất đường phân giác trong tam giác)
Xét tam giác BCD với đường phân giác BE, ta có:
\(\frac{{ED}}{{EC}} = \frac{{BD}}{{BC}}\,\,\left( 2 \right)\) (Tính chất đường phân giác trong tam giác)
Từ (1) và (2) ta có: \(\frac{{AD}}{{AC}} = \frac{{BD}}{{BC}} \Rightarrow AD.BC = AC.BD\)