
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đây là đẳng thức ptôlêmê.
C/m: Lấy 1 điểm M thuộc AC sao cho gocABD=gocMBC. Do tứ giác ABCD nội tiếp nên ^ADC=^ACB. Từ 2 điều trên suy ra tam giác ABD ~ MBC(g.g). Suy ra AD/MC=BD/BC => AD.BC=BD.MC (1)
Từ cặp tam giác đồng dạng trên ta cũng có AB/BM = BD/BC => AB/BD = BM/BC mà ^ABM = ^DBC nên tam giác ABM ~ tam giác DBC.
=> AB.CD=AM.BD (2)
Cộng (1), (2) vế theo vế suy ra AC.BD = AB . CD + AD . BC
Vậy AC.BD = AB.CD + AD . BC ( đpcm )

A B C D M N I
Nối đường chéo BD của tứ giác ABCD. Lấy I là trung điểm của đoạn BD, nối IM và IN.
Xét \(\Delta\)BAD: I là trung điểm BD; M là trung điểm AD => IM là đường trung bình của tam giác BAD
=> IM = 1/2 AB. Tương tự ta có: IN = 1/2 CD \(\Rightarrow IM+IN=\frac{AB+CD}{2}\)
Mà \(IM+IN\ge MN\)(T/c 3 điểm) \(\Rightarrow\frac{AB+CD}{2}\ge MN\)
Vậy \(MN\le\frac{AB+CD}{2}\)(đpcm).
Dấu "=" xảy ra <=> I thuộc đoạn MN <=> MN // AB // CD (Do IM // AB và IN // CD) <=> Tứ giác ABCD là hình thang.

Gọi M là trung điểm của AC, ta có:
\(GE\le GM+ME=\dfrac{1}{2}CD+\dfrac{1}{2}AB=\dfrac{AB+CD}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow\) Ba điểm M, G, E thẳng hàng.
\(\Leftrightarrow\) GE // AB và GE // CD \(\Leftrightarrow\) AB // CD
\(\Leftrightarrow\) Tứ giác ABCD là hình thang.
A B C D E G M

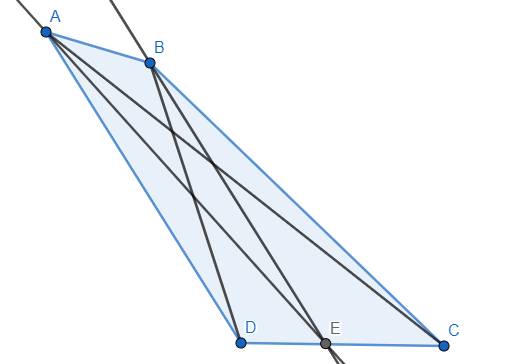
Áp dụng tính chất tia phân giác, ta có \(\dfrac{ED}{EC}=\dfrac{AD}{AC}\) và \(\dfrac{ED}{EC}=\dfrac{BD}{BC}\). Từ đó suy ra \(\dfrac{AD}{AC}=\dfrac{BD}{BC}\Rightarrow AD.BC=AC.BD\) (đpcm)
Sử dụng tính chất tam giác đồng dạng và bất đẳng thức tam giác.
Dựng điểm E sao cho tam giác BCD đồng dạng với tam giác BEA. Khi đó, theo tính chất của tam giác đồng dạng, ta có
\(\frac{BA}{EA}=\frac{BD}{CD}\)
Suy ra \(BA.CD=EA.BD\left(1\right)\)
Mặt khác, tam giác EBC và tam giác ABD cũng đồng dạng do có
\(\frac{BA}{BD}=\frac{BE}{BC}\) và góc EBC= góc ABD
Từ đó
\(\frac{EC}{BC}=\frac{AD}{BD}\)
Suy ra
\(AD.BC=EC.BD\left(2\right)\)
Cộng (1) và (2) ta suy ra
\(AB.CD+AD.BC=BD.\left(EA+EC\right)\)
Áp dụng bất đẳng thức tam giác ta suy ra \(AB.CD+AD>BC\ge AC>BD\)
Dấu bằng xảy ra khi và chỉ khi tứ giác nội tiếp trong một đường tròn và trở thành định lý Ptoleme.
Lớp 8 đã học tứ giác nội tiếp đâu mà bạn đã kết luận như vậy rồi.Bạn làm theo ý tưởng trên Wikipedia cũng phải chỉ rõ cách dựng điểm E ; kết luận dấu = xảy ra khi E,C,A thẳng hàng rồi từ đó suy ra tổng 2 góc đối của tứ giác bằng 1800