Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


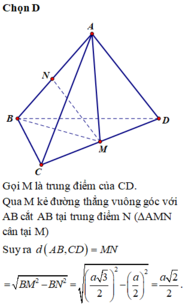
Hai tam giác CBA và DBA là hai tam giác đều cạnh a
=> ∆ CBA = ∆ DBA ( c.c.c)
=> CM = DM ( 2 đường trung tuyến tương ứng)
=> Tam giác CMD cân tại M.
Lại có: MN là đường trung tuyến nên đồng thời là đường cao: MN ⊥ CD
* Chứng minh tương tự, ta có: MN ⊥ AB
Do đó, MN là đoạn vuông góc chung của AB và CD.
* Tam giác BCD là tam giác đều cạnh a nên


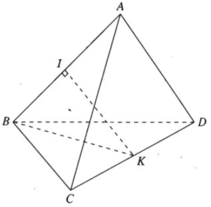
Giả thiết cho ABCD là tứ diện đều nên các cặp cạnh đối diện của tứ diện đó có vai trò như nhau. Do đó ta chỉ cần tính khoảng cách giữa hai cạnh AB và CD là đủ.
Gọi I và K lần lượt là trung điểm của AB và CD. Dễ thấy IK là đoạn vuông góc chung của AB và CD nên nó chính là khoảng cách giữa AB và CD.
Tam giác BKI vuông tại I. Ta có :
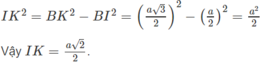

Đáp án B
Gọi O là trọng tâm ∆ABC
Kẻ AM ⊥ AC và MH ⊥ AD
Vì DABC là tứ diện đều => DO ⊥ (ABC)
Vì ∆ABC đều => AO = ![]()
Xét ∆DAO vuông tại O

Ta có: DO ⊥ BC và AM ⊥ BC
=> (DAM) ⊥ BC
=> MH ⊥ BC
Lại có MH ⊥ DA
=> MH = d(BC, DA)
Xét ∆DAM, ta có:
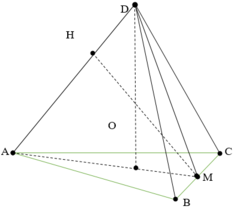
DO.AM = MH.AD
⇔ MH = a 2 2
⇔ d(BC, DA) = a 2 2

Đáp án B.
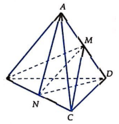
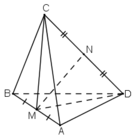
Gọi lần lượt là trung điểm của AD và BC. Ta có ∆ ABD và ∆ ACD đều cạnh bằng a nên
![]()
=> ∆ MBC cân tại M và MN là đường cao của ∆ MBC => MN ⊥ BC
Tương tự, ∆ NAD cân tại N nên NM là đường cao của ∆ NAD => NM ⊥ AD
Suy ra MN là đoạn vuông góc cung của AD và BC.
Vậy
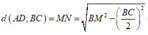
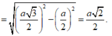

Hai tam giác CBA và DBA là hai tam giác đều cạnh a
=> ∆ CBA = ∆ DBA ( c.c.c)
=> CM = DM ( 2 đường trung tuyến tương ứng)
=> Tam giác CMD cân tại M.
Lại có: MN là đường trung tuyến nên đồng thời là đường cao: MN ⊥ CD
* Chứng minh tương tự, ta có: MN ⊥ AB
Do đó, MN là đoạn vuông góc chung của AB và CD.
* Tam giác BCD là tam giác đều cạnh a nên
\(BN=\sqrt{BC^2-CN^2}=\frac{a\sqrt{3}}{2}\)
Bài này học rồi mà bà

Đặt \(\overrightarrow{DA}=\)\(\overrightarrow{a}\) , \(\overrightarrow{DB}=\overrightarrow{b},\overrightarrow{DC}=\overrightarrow{c}\) với \(\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=\left|\overrightarrow{c}\right|=a\) và \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=\frac{a^2}{2}\) như hình vẽ
Do M là trung điểm AB nên \(\overrightarrow{DM}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}\)
do đó \(\overrightarrow{CM}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}-\overrightarrow{c}\)
Xét điểm \(N\in AC\), giả sử \(\overrightarrow{NA}=t.\overrightarrow{NC}\), \(t\ne1\). Khi đó \(\overrightarrow{DN}=\frac{\overrightarrow{a}-t\overrightarrow{c}}{1-t}\)
Vậy \(DN\perp CM\Rightarrow\overrightarrow{DN}.\overrightarrow{CM}=0\Leftrightarrow\left(\overrightarrow{a}+\overrightarrow{b}-2\overrightarrow{c}\right)\left(\overrightarrow{a}-t\overrightarrow{c}\right)=0\Leftrightarrow t=\frac{1}{2}\)
Từ đó , với \(N\in AC\) mà \(\overrightarrow{NC}=-2\overrightarrow{NA}\) thì \(DN\perp CM\) và khi đó
\(\overrightarrow{DN}=\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{c}\)
Giả sử UV là đoạn vuông góc chung của CM, DN với \(U\in CM,V\in DN\) và \(\overrightarrow{CU}=u\overrightarrow{CM}=\frac{u}{2}.\overrightarrow{a}+\frac{u}{2}.\overrightarrow{b}-u.\overrightarrow{c},\overrightarrow{DV}=v.\overrightarrow{DN}=\frac{2v}{3}.\overrightarrow{a}+\frac{v}{3}.\overrightarrow{c}\)
Từ đó suy ra
\(\overrightarrow{UV}=\overrightarrow{DV}-\left(\overrightarrow{DC}+\overrightarrow{CU}\right)\)
\(=\left(\frac{2v}{3}-\frac{u}{2}\right)\overrightarrow{a}-\frac{u}{2}\overrightarrow{b}+\left(\frac{v}{3}+u-1\right)\overrightarrow{c}\)
Điều kiện \(\overrightarrow{UV}.\overrightarrow{CM}=0\) tương đương với :
\(\frac{1}{2}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{4}-\left(\frac{v}{3}+u-1\right)+\frac{1}{4}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{1}{2}\left(\frac{2v}{3}-\frac{u}{2}\right)+\frac{u}{4}+\frac{1}{4}\left(\frac{v}{3}+u-1\right)+\frac{1}{4}\left(\frac{v}{3}+u-1\right)=0\)
Từ đó ta thu được \(u=\frac{2}{3}\)
Điều kiện \(\overrightarrow{UV}.\overrightarrow{DN}=0\) tương đương với :
\(\frac{2}{3}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{6}+\frac{1}{3}\left(\frac{v}{3}+u-1\right)+\frac{1}{6}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{12}+\frac{1}{3}\left(\frac{v}{3}+u-1\right)=0\)
Từ đó ta thu được \(v=\frac{6}{7}\)
Khi đó, \(\overrightarrow{UV}=\frac{5}{21}\overrightarrow{a}-\frac{7}{21}\overrightarrow{b}-\frac{1}{21}\overrightarrow{c}=\frac{1}{21}\left(5\overrightarrow{a}-7\overrightarrow{b}-\overrightarrow{c}\right)\)
Suy ra \(d\left(CM,DN\right)=UV=\sqrt{\left|\overrightarrow{UV}\right|^2}=\frac{a\sqrt{42}}{21}\)

Đáp án C
Khoảng cách từ B bằng với chiều cao của tứ diện đều ABCD. Do đó ta dễ dàng suy ra được:
![]()
=> Chọn phương án C.