
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đặt \(\overrightarrow{DA}=\)\(\overrightarrow{a}\) , \(\overrightarrow{DB}=\overrightarrow{b},\overrightarrow{DC}=\overrightarrow{c}\) với \(\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=\left|\overrightarrow{c}\right|=a\) và \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=\frac{a^2}{2}\) như hình vẽ
Do M là trung điểm AB nên \(\overrightarrow{DM}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}\)
do đó \(\overrightarrow{CM}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}-\overrightarrow{c}\)
Xét điểm \(N\in AC\), giả sử \(\overrightarrow{NA}=t.\overrightarrow{NC}\), \(t\ne1\). Khi đó \(\overrightarrow{DN}=\frac{\overrightarrow{a}-t\overrightarrow{c}}{1-t}\)
Vậy \(DN\perp CM\Rightarrow\overrightarrow{DN}.\overrightarrow{CM}=0\Leftrightarrow\left(\overrightarrow{a}+\overrightarrow{b}-2\overrightarrow{c}\right)\left(\overrightarrow{a}-t\overrightarrow{c}\right)=0\Leftrightarrow t=\frac{1}{2}\)
Từ đó , với \(N\in AC\) mà \(\overrightarrow{NC}=-2\overrightarrow{NA}\) thì \(DN\perp CM\) và khi đó
\(\overrightarrow{DN}=\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{c}\)
Giả sử UV là đoạn vuông góc chung của CM, DN với \(U\in CM,V\in DN\) và \(\overrightarrow{CU}=u\overrightarrow{CM}=\frac{u}{2}.\overrightarrow{a}+\frac{u}{2}.\overrightarrow{b}-u.\overrightarrow{c},\overrightarrow{DV}=v.\overrightarrow{DN}=\frac{2v}{3}.\overrightarrow{a}+\frac{v}{3}.\overrightarrow{c}\)
Từ đó suy ra
\(\overrightarrow{UV}=\overrightarrow{DV}-\left(\overrightarrow{DC}+\overrightarrow{CU}\right)\)
\(=\left(\frac{2v}{3}-\frac{u}{2}\right)\overrightarrow{a}-\frac{u}{2}\overrightarrow{b}+\left(\frac{v}{3}+u-1\right)\overrightarrow{c}\)
Điều kiện \(\overrightarrow{UV}.\overrightarrow{CM}=0\) tương đương với :
\(\frac{1}{2}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{4}-\left(\frac{v}{3}+u-1\right)+\frac{1}{4}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{1}{2}\left(\frac{2v}{3}-\frac{u}{2}\right)+\frac{u}{4}+\frac{1}{4}\left(\frac{v}{3}+u-1\right)+\frac{1}{4}\left(\frac{v}{3}+u-1\right)=0\)
Từ đó ta thu được \(u=\frac{2}{3}\)
Điều kiện \(\overrightarrow{UV}.\overrightarrow{DN}=0\) tương đương với :
\(\frac{2}{3}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{6}+\frac{1}{3}\left(\frac{v}{3}+u-1\right)+\frac{1}{6}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{12}+\frac{1}{3}\left(\frac{v}{3}+u-1\right)=0\)
Từ đó ta thu được \(v=\frac{6}{7}\)
Khi đó, \(\overrightarrow{UV}=\frac{5}{21}\overrightarrow{a}-\frac{7}{21}\overrightarrow{b}-\frac{1}{21}\overrightarrow{c}=\frac{1}{21}\left(5\overrightarrow{a}-7\overrightarrow{b}-\overrightarrow{c}\right)\)
Suy ra \(d\left(CM,DN\right)=UV=\sqrt{\left|\overrightarrow{UV}\right|^2}=\frac{a\sqrt{42}}{21}\)

11.
\(SA\perp\left(ABCD\right)\Rightarrow\) AC là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(\Rightarrow\widehat{SCA}=\varphi\)
\(AC=BD=\sqrt{AB^2+AD^2}=a\sqrt{13}\)
\(tan\varphi=\frac{SA}{AC}=\frac{\sqrt{13}}{13}\)
12.
Hai vecto \(\overrightarrow{AB}\) và \(\overrightarrow{EF}\) song song cùng chiều
\(\Rightarrow\left(\overrightarrow{AB};\overrightarrow{EG}\right)=\left(\overrightarrow{EF};\overrightarrow{EG}\right)=\widehat{GEF}=45^0\)
8.
Qua O có 1 và chỉ 1 mặt phẳng vuông góc \(\Delta\)
9.
Gọi O là tâm tam giác BCD
\(\Rightarrow AO\perp\left(BCD\right)\Rightarrow AO\perp CD\)
Mà \(CD\perp BO\) (trung tuyến đồng thời là đường cao)
\(\Rightarrow CD\perp\left(ABO\right)\Rightarrow CD\perp AB\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{CD}=0\)
10.
\(AB\perp AD\Rightarrow\widehat{BAD}=90^0\)

Câu 8:
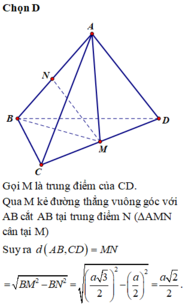
Kẻ \(AH\perp SM\)
Trong mặt phẳng (SBC), qua H kẻ đường thẳng song song BC cắt SB và SC lần lượt tại P và Q
\(\Rightarrow\Delta APQ\) là thiết diện của (P) và chóp
\(AM=\frac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow SA=AM\Rightarrow\Delta SAM\) vuông cân tại A
\(\Rightarrow AH=\frac{SA\sqrt{2}}{2}=\frac{a\sqrt{6}}{4}\) đồng thời H là trung điểm SM
\(\Rightarrow PQ=\frac{1}{2}BC=\frac{a}{2}\) (đường trung bình)
\(\Rightarrow S_{\Delta APQ}=\frac{1}{2}AH.PQ=\frac{a^2\sqrt{6}}{16}\)
Câu 9.
\(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(SH=AH=\frac{a\sqrt{3}}{2}\Rightarrow\Delta SAH\) vuông cân tại H
\(\Rightarrow\widehat{SAH}=45^0\)
Câu 6:
Bạn kiểm tra lại đề, \(SO\perp\left(ABCD\right)\Rightarrow SO\perp OB\Rightarrow\widehat{SOB}=90^0\)
Nên không thể có chuyện \(tan\widehat{SOB}=\frac{1}{2}\)
Câu 7:
H là trực tâm tam giác ABC \(\Rightarrow BH\perp AC\)
Mà \(SA\perp\left(ABC\right)\Rightarrow SA\perp BH\)
\(\Rightarrow BH\perp\left(SAC\right)\Rightarrow BH\perp SC\) (1)
K là trực tâm tam giác SBC \(\Rightarrow BK\perp SC\) (2)
(1);(2) \(\Rightarrow SC\perp\left(BHK\right)\Rightarrow\) góc giữa SC và (BHK) bằng 90 độ

16.
Đặt cạnh của đáy là x
\(DM=\sqrt{AD^2+AM^2}=\sqrt{x^2+\left(\frac{x}{2}\right)^2}=\frac{x\sqrt{5}}{2}\)
\(CM=\sqrt{BC^2+BM^2}=\sqrt{x^2+\left(\frac{x}{2}\right)^2}=\frac{x\sqrt{5}}{2}\)
\(\Rightarrow DM=CM\Rightarrow\Delta_vSMD=\Delta_vSMC\)
\(\Rightarrow SC=SD=2a\sqrt{5}\)
Mà \(SM\perp\left(ABCD\right)\Rightarrow\widehat{SCM}\) là góc giữa SC và (ABCD) \(\Rightarrow\widehat{SCM}=60^0\)
\(\Rightarrow\left\{{}\begin{matrix}CM=SC.cos60^0=a\sqrt{5}\\SM=SC.sin60^0=a\sqrt{15}\end{matrix}\right.\) \(\Rightarrow AB=x=\frac{2CM}{\sqrt{5}}=2a\)
Gọi N là trung điểm CD \(\Rightarrow CD\perp\left(SMN\right)\)
\(AM//CD\Rightarrow AM//\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(M;\left(SCD\right)\right)\)
Từ M kẻ \(MM\perp SN\Rightarrow MH\perp\left(SCD\right)\Rightarrow MH=d\left(H;\left(SCD\right)\right)\)
\(MN=AB=2a\)
\(\frac{1}{MH^2}=\frac{1}{SM^2}+\frac{1}{MN^2}\Rightarrow MH=\frac{SM.MN}{\sqrt{SM^2+MN^2}}=\frac{2a\sqrt{15}}{\sqrt{19}}\)
14.
Do \(\widehat{C'BC}\) là góc giữa (ABCD) và (ABC') nên \(\widehat{C'BC}=60^0\)
\(\Rightarrow CC'=BC.tan60^0=a\sqrt{3}\)
15.
Gọi H là trung điểm BC \(\Rightarrow OH\perp BC\)
Chóp tứ giác đều \(\Rightarrow SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
\(\Rightarrow BC\perp\left(SOH\right)\)
Từ O kẻ \(OK\perp SH\Rightarrow OK\perp\left(SBC\right)\Rightarrow OK=d\left(O;\left(SBC\right)\right)\)
\(OH=\frac{1}{2}AB=\frac{a}{2}\) ; \(AC=a\sqrt{2}\Rightarrow OA=\frac{a\sqrt{2}}{2}\)
\(SO=\sqrt{SA^2-OA^2}=\frac{a\sqrt{2}}{2}\)
\(\frac{1}{OK^2}=\frac{1}{SO^2}+\frac{1}{OH^2}\Rightarrow OK=\frac{SO.OH}{\sqrt{SO^2+OH^2}}=\frac{a\sqrt{6}}{6}\)

Tao có: \(\overrightarrow{BC}.\overrightarrow{AD}=\overrightarrow{BC}\left(\overrightarrow{DC}+\overrightarrow{CA}\right)=\overrightarrow{CB}.\overrightarrow{CD}-\overrightarrow{CB}.\overrightarrow{CA}\)
\(=\frac{1}{2}\left(CB^2+CD^2-BD^2\right)-\frac{1}{2}\left(CB^2+CA^2-AB^2\right)\)
\(=\frac{1}{2}\left(AB^2+CD^2-BD^2-CA^2\right)\)
\(\Rightarrow\cos\left(\overrightarrow{BC},\overrightarrow{DA}\right)=\frac{1}{2}.\frac{c^2+c'^2-b^2-b'^2}{2aa'}\)

Câu 1:
\(CD//AB\Rightarrow\) góc giữa SB và CD bằng góc giữa SB và AB
Mà \(\widehat{SBA}\) là góc giữa SB và AB
\(tan\widehat{SBA}=\frac{SA}{AB}=\frac{\sqrt{3}AB}{AB}=\sqrt{3}\Rightarrow\widehat{SBA}=60^0\)
Câu 2:
\(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=AB\sqrt{2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\frac{SA}{AC}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)