

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
Ta tìm số cặp số (a;b) thoả mãn
![]()
![]()
Có 49 cặp (a;b) thỏa mãn. Do đó S gồm 49 phần tử:
Ta tìm số cặp (a;b) thoả mãn
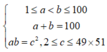
![]()
Do đó 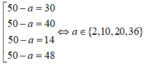
Vậy có 4 cặp số (a;b)có tổng bằng 100 và tích của chúng là một số chính phương.

Đáp án B.
Số phần tử của E là ![]() .
.
Từ 5 chữ số đã cho ta có 4 bộ gồm 3 chữ số có tổng chia hết cho 3 là ![]() . Mỗi bộ 3 chữ số này ta lập được
. Mỗi bộ 3 chữ số này ta lập được ![]() số thuộc tập hợp E. Vậy trong tập hợp E có
số thuộc tập hợp E. Vậy trong tập hợp E có ![]() số chia hết cho 3.
số chia hết cho 3.
Gọi A là biến cố “Số được chọn từ E chia hết cho 3” thì ![]() .
.
Vậy xác suất cần tính là 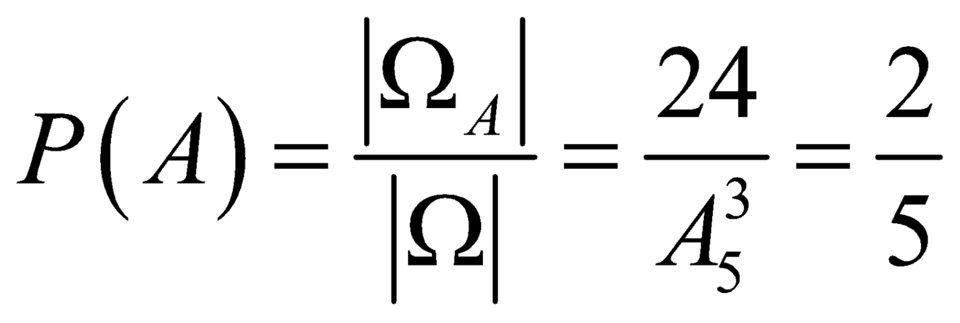 .
.

Đáp án B
Số phần tử của tập hợp M là: C 15 3
Gọi O là tâm đường tròn ngoại tiếp của đa giác đều, Xét một đỉnh A bất kỳ của đa giác: Có 7 cặp đỉnh của đa giác đối xứng với nhau qua đường thẳng OA, hay có 7 tam giác cân tại đỉnh A. Như vậy, với mỗi một đỉnh của đa giác có 7 tam giác nhận nó làm đỉnh tam giác cân.
Số tam giác đều có 3 đỉnh là các đỉnh của đa giác là 15 3 = 5 tam giác.
Tuy nhiên, trong các tam giác cân đã xác định ở trên có cả tam giác đều, do mọi tam giác đều thì đều cân tại 3 đỉnh nên tam giác đều được đếm 3 lần.
Suy ra, số tam giác cân nhưng không phải tam giác đều có 3 đỉnh là 3 đỉnh của đa giác đã cho là: 7.15 – 3.5 = 90
Do đó xác suất cần tìm là P = 90 C 15 3 = 18 91 .

Đáp án C
Số tập con của A là 2 6
Số tập con gồm đúng 2 phần tử của A là C 6 2
Xác suất cần tính bằng C 6 2 2 6 = 15 64

Chọn B
Số tập con của S là 2 6 = 64
Mỗi người có 64 cách chọn tập con, do vậy số phần tử của không gian mẫu là: 64 2
Ta tìm số cách chọn tập con thỏa mãn yêu cầu:
Giả sử tập con của A và B chọn được lần lượt có x,y phần tử ![]()
Khi đó: A có C 6 x cách chọn tập con, lúc này S còn 6 - x phần tử.
Ta chọn ra 2 phần tử gọi là a,b từ x phần tử trong tập con của A để xuất hiện trong tập con của B, có C x 2 cách.
Như vậy, tập con của B đã có 2 phần tử chung với tập con của A là a,b ta cần chọn thêm (y-2) phần tử khác trong (6-x) phần tử còn lại sau khi A đã chọn tập con,ở bước này có C 6 - x y - 2 cách chọn.
Vậy có: C 6 x C 6 - x y - 2 cách chọn tập con thỏa mãn.
Ta có điều kiện:
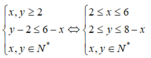
Cho x nhận các giá trị từ 2 đến 6, số cách chọn tập con thỏa mãn yêu cầu đề bài là:
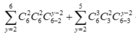
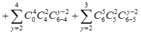
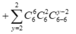
= 240 + 480 + 360 + 120 + 15 = 1215
Xác suất cần tính bằng: 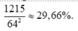

Đáp án C

Gọi A là biến cố: “Chọn được tam giác vuông”
Đa giác đều 4n đỉnh nội tiếp trong đường tròn tâm O có 2n đường chéo qua tâm O .
Mỗi tam giác vuông tạo bởi hai đỉnh nằm trên cùng một đường chéo qua tâm O và một đỉnh trong 4 n - 2 đỉnh còn lại.
Suy ra số tam giác vuông được tạo thành là C 2 n 1 . C 4 n - 2 1 .
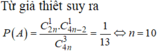

Số phần tử của S là: \(8!\)
Gọi tổng 4 chữ số sau là S \(\Rightarrow\) tổng 4 chữ số đầu là \(S+2\)
Ta có: \(S+S+2=1+3+4+5+6+7+8+9\)
\(\Rightarrow2S=41\Rightarrow S=\dfrac{41}{2}\) (vô lý do các chữ số đều nguyên)
Vậy đề bài sai