Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
Dựng hình bình hành ABCD \(\Rightarrow\left|\overrightarrow{BM}+\overrightarrow{BA}\right|=\left|\overrightarrow{MC}+\overrightarrow{CD}\right|=MD\)
Hạ ME vuông góc với CD \(\Rightarrow CE=ME=\frac{1}{2}AC\) và \(DE=CD+CE\)
\(\Delta ABC\) vuông cân tại A, theo Pytago ta có:
\(AC=\frac{\sqrt{BC^2}}{2}=a\)
\(\Rightarrow ME=\frac{a}{2}\) và \(DE=CE+CD=\frac{a}{2}+a=\frac{3a}{2}\)
\(\Delta EDM\) vuông tại E, theo Pytago ta có:
\(MD=\sqrt{ME^2+ED^2}=\sqrt{\frac{a^2}{4}+\frac{9a^2}{4}}=\frac{a\sqrt{10}}{2}\)
Câu 2:
Dựng \(\overrightarrow{OC}=\frac{11}{4}\overrightarrow{OA}\Rightarrow OC=\frac{11}{4}a\), \(\overrightarrow{OD}=\frac{3}{7}\overrightarrow{OB}\Rightarrow OD=\frac{3}{7}a\)
Ta có:
\(\left|\overrightarrow{v}\right|=\left|\frac{11}{4}\overrightarrow{OA}-\frac{3}{7}\overrightarrow{OB}\right|=\left|\overrightarrow{OC}-\overrightarrow{OD}\right|=\left|\overrightarrow{DC}\right|=DC\)
Tam giác OCD vuông tại O, theo Pytago, ta có:
\(DC=\sqrt{OD^2+OC^2}=\sqrt{\frac{9a^2}{49}+\frac{121a^2}{16}}\)\(=a\sqrt{\frac{6073}{784}}\)

Ta có:
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AO}+\overrightarrow{AB}\right)\)
\(\Leftrightarrow\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AO}+\overrightarrow{AO}+\overrightarrow{OB}\right)\)
\(\Leftrightarrow\overrightarrow{AM}=\dfrac{1}{2}\left(2\overrightarrow{AO}+\overrightarrow{OB}\right)\)
\(\Leftrightarrow\overrightarrow{AM}=\overrightarrow{AO}+\dfrac{1}{2}\overrightarrow{OB}\)
\(\Leftrightarrow\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{OB}-\overrightarrow{OA}\)
\(\RightarrowĐPCM\)
Câu b ) Bạn làm tương tự câu a , ta có vecto BN = 1/2 (BO +BC ) , rồi là như câu a
chúc bạn hok tốt

a: \(\overrightarrow{AM}+\overrightarrow{BN}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\overrightarrow{AC}\)
b: \(=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BA}\)
\(=\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BA}\)
c: \(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{CA}\)
\(=\dfrac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CA}\right)=\overrightarrow{0}\)

Lời giải:
a) Bạn tham khảo tại đây:
Câu hỏi của Trần Thị Như Ý - Toán lớp 10 | Học trực tuyến
b)
\(|\overrightarrow{OB}+\overrightarrow{AC}-\overrightarrow{OA}|=|\overrightarrow{OB}+\overrightarrow{AO}+\overrightarrow{OC}-\overrightarrow{OA}|\)
\(=|\overrightarrow{OB}+\overrightarrow{OC}-2\overrightarrow{OA}|\)
\(=|-\overrightarrow{OA}-2\overrightarrow{OA}|=3|\overrightarrow{OA}|=3a\)
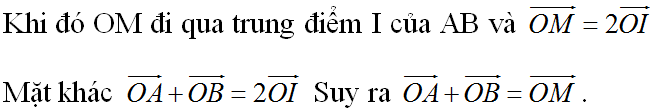
b)
O B A M N
\(\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AO}=-\dfrac{1}{2}\overrightarrow{OA}\)
Vậy \(m=-\dfrac{1}{2};n=0\).
c)
\(\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{AB}=\dfrac{1}{2}\left(\overrightarrow{AO}+\overrightarrow{OB}\right)=-\dfrac{1}{2}\overrightarrow{OA}+\dfrac{1}{2}\overrightarrow{OB}\).
Vậy \(m=-\dfrac{1}{2};n=\dfrac{1}{2}\).
d)
\(\overrightarrow{MB}=\dfrac{1}{2}\overrightarrow{OB}\)
Vậy \(m=0;n=\dfrac{1}{2}\).