Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

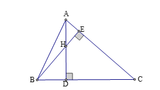
Xét tam giác vuông ABD và ADC, ta có: tan B = A D B D ; tan C = A D C D
Suy ra: tan B . tan C = A D 2 B D . C D (1)
Lại có H B D ^ = C A D ^ (cùng phụ với A C B ^ ) và H D B ^ = A D C ^ = 90 0
Do đó ∆ B D H ~ ∆ A D C (g.g), suy ra D H D C = B D A D , do đó BD.DC = DH.AD (2)
Từ (1) và (2) suy ra tan B . tan C = A D 2 D H . A D = A D D H (3)
Theo giả thiết H D A H = 3 2 suy ra H D A H + H D = 3 2 + 3 hay H D A D = 3 5 , suy ra AD = 5 3 HD
Thay vào (3) ta được: tan B . tan C = 5 3 H D D H = 5 3
Đáp án cần chọn là: D

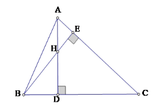
Xét tam giác vuông ABD và ADC, ta có tan B = A D B D ; tan C = A D C D
Suy ra: tan B . tan C = A D 2 B D . C D (1)
Lại có: H B D ^ = C A D ^ (cùng phụ với A C B ^ ) và H D B ^ = A D C ^ = 90 0
Do đó ∆ B D H ~ ∆ A D C (g.g), suy ra D H D C = B D A D , do đó BD.DC = DH.AD (2)
Từ (1) và (2) suy ra tan B . tan C = A D 2 D H . A D = A D D H (3)
Theo giả thiết H D A H = 1 2 suy ra H D A H + H D = 1 2 + 1 hay H D A D = 1 3 , suy ra AD = 3HD
Thay vào (3) ta được: tan B . tan C = 3 H D D H = 3
Đáp án cần chọn là: B

Lời giải:
Xét tam giác vuông $ABD$:
$\tan B=\frac{AD}{BD}(1)$
Lại có:
$\widehat{C}=\widehat{BHD}(=90^0-\widehat{EBC})$
$\Rightarrow \tan C=\tan \widehat{BHD}=\frac{BD}{HD}(2)$
Từ $(1);(2)\Rightarrow \tan B.\tan C=\frac{AD}{BD}.\frac{BD}{HD}=\frac{AD}{HD}$ (đpcm)

a) Xét \(\Delta BAE\) và \(\Delta CAF\) có:
\(\widehat{A}\) chung
\(\widehat{AEB}=\widehat{CFA}=90^0\)
nên \(\Delta BAE\sim\Delta CAF\left(g.g\right)\) \(\Rightarrow\dfrac{BA}{CA}=\dfrac{AE}{AF}\)\(\Leftrightarrow\dfrac{AB}{AE}=\dfrac{AC}{AF}\)
Xét \(\Delta ABC\) và \(\Delta AEF\) có:
Góc A chung
\(\dfrac{AB}{AE}=\dfrac{AC}{AF}\)
nên \(\Delta ABC\sim\Delta AEF\left(c.g.c\right)\) \(\Rightarrow\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AE}{AB}\right)^2=cos^2A=\dfrac{1}{2}\)
\(\Rightarrow2S_{AEF}=S_{ABC}=S_{AEF}+S_{BFEC}\) \(\Leftrightarrow S_{AEF}=S_{BFEC}\) (dpcm)
b) Có \(\widehat{AFE}=\widehat{ACB}\) (do \(\Delta ABC\sim\Delta AEF\))
\(\Leftrightarrow90^0-\widehat{AFE}=90^0-\widehat{ACB}\)
\(\Leftrightarrow\widehat{EFC}=\widehat{DAC}\) mà \(\widehat{C}\) chung \(\Rightarrow\Delta EFC\sim\Delta HAC\left(g.g\right)\)
\(\Rightarrow\dfrac{EF}{HA}=\dfrac{FC}{AC}\)\(\Leftrightarrow\dfrac{EF}{HA}=sinA\)\(\Leftrightarrow EF=HA.sinA\)
c)CM được:\(\Delta DHC\sim\Delta FBC\left(g.g\right)\)\(\Rightarrow\dfrac{HD}{BF}=\dfrac{CH}{BC}\Leftrightarrow\dfrac{HD.BC}{BF}=CH\)
\(\Delta HEC\sim\Delta AFC\left(g.g\right)\)\(\Rightarrow\dfrac{HE}{AF}=\dfrac{HC}{AC}\) \(\Leftrightarrow\dfrac{HE.AC}{AF}=HC\)
Xét \(S_{BHC}.tanB-S_{HAC}.tanA\)\(=\dfrac{1}{2}.HD.BC.\dfrac{FC}{BF}-\dfrac{1}{2}.HE.AC.\dfrac{FC}{AF}\)
\(=\dfrac{1}{2}.CH.FC-\dfrac{1}{2}.HC.FC=0\) \(\Leftrightarrow S_{BHC}.tanB-S_{HAC}.tanA=0\)
\(\Leftrightarrow\dfrac{S_{BHC}}{tanA}=\dfrac{S_{HAC}}{tanB}\) , CM tương tự \(\Rightarrow\dfrac{S_{HAC}}{tanB}=\dfrac{S_{HAB}}{tanC}\)
=>dpcm

Mình có nghe nói là 2 nhà toán học Alfred North Whitehead và Bertrand Russell đã chứng minh 1+1=2 trong quyển Principa Mathemaa (tạm dịch: nền tảng của toán học). Họ đã mất hơn 360 trang để chứng minh điều này. Thầy giáo bạn gãi đầu là phải.
Phép chứng minh này dựa trên một bộ 9 tiên đề về tập hợp gọi tắt là ZFC (Zermelo–Fraenkel). Rất nhiều lý thuyết số học hiện đại dựa trên những tiên đề này. Nếu có người chứng minh được một trong những tiên đề đó là sai (VD: 2 tập hợp có cùng các phần tử mà vẫn không bằng nhau) thì rất có thể dẫn đến 1+1 != 2