Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C O I H M N
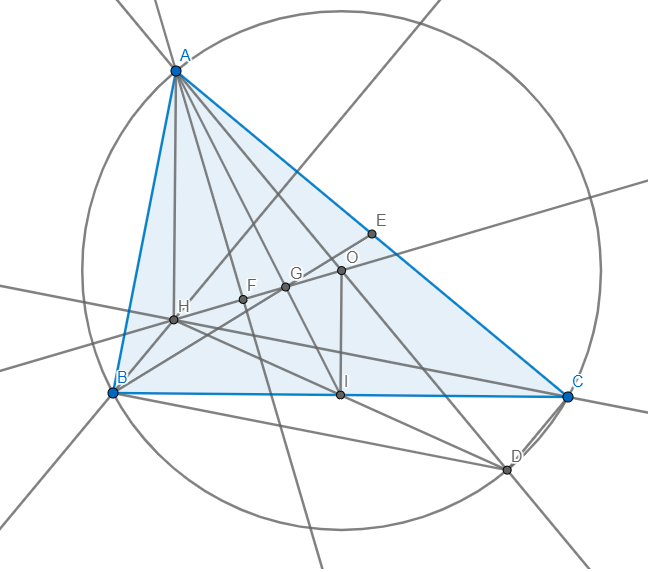
Gọi N là trung điểm của AC. Nối N với O và M.
Do H là trực tâm \(\Delta\)ABC => ^BAH + ^ABC = 900 (1)
Dễ thấy MN là đường trung bình \(\Delta\)ABC => MN // AB => ^NMC = ^ABC (2)
Lại có: ^NMO + ^NMC = 900 (3)
Từ (1); (2) và (3) => ^BAH = ^NMO. Tương tự: ^ABH = ^MNO
=> \(\Delta\)AHB ~ \(\Delta\)MON (g.g) => \(\frac{AH}{MO}=\frac{AB}{MN}=2\)(Do MN là đg trung bình \(\Delta\)ABC)
\(\Rightarrow\frac{AH}{MO}=\frac{AI}{MI}=2\)(Vì I là trọng tâm và AM là trung tuyến \(\Delta\)ABC)
Xét \(\Delta\)AHI và \(\Delta\)MOI: ^HAI = ^OMI (Do AH // OM); \(\frac{AH}{MO}=\frac{AI}{MI}\)=> \(\Delta\)AHI ~ \(\Delta\)MOI (c.g.c)
\(\Rightarrow\frac{IH}{IO}=\frac{IA}{IM}=2\Rightarrow IH^2=4.IO^2\).Tương tự \(HA^2=4.OM^2\)
\(\Rightarrow\sqrt{\frac{IO^2+OM^2}{IH^2+HA^2}}=\sqrt{\frac{IO^2+OM^2}{4\left(IO^2+OM^2\right)}}=\frac{1}{2}.\)
ĐS: 1/2.

H I O A B C M K
Dựng hình vẽ như trên. Dễ thấy O là tâm của đường tròn ngoại tiếp tam giác ABC => OA = OK và OM vuông góc BC
=> OM là đường trung bình của tam giác AHK => OM // AH và OM = 1/2AH
Dễ dàng chứng minh được O,I,H thẳng hàng và OH vuông góc OM , AH vuông góc HI
Ta có : \(\sqrt{\frac{OI^2+OM^2}{IH^2+HA^2}}=\sqrt{\frac{IM^2}{AI^2}}=\frac{IM}{AI}=\frac{1}{2}\)

Dạ anh ơi, phiền anh câu này nữa ạ
Nguyễn Việt Lâm
Anh giúp em với, hai ngày nữa em thi HSG rồi![]()
Bạn tự vẽ hình
O là giao điểm 3 đường trung trực =>O là tâm đường tròn ngoại tiếp tam giác \(\Rightarrow OM\perp BC\)
H là trực tâm \(\Rightarrow AH\perp BC\Rightarrow\) AH//OM
Gọi N là trung điểm AC \(\Rightarrow\) MN//AB
\(\Rightarrow\widehat{BAH}=\widehat{OMN}\) (góc có cạnh tương ứng song song)
Tương tự ta có ON//BH \(\Rightarrow\widehat{ONM}=\widehat{ABH}\) (vẫn là góc có cạnh tương ứng song song)
\(\Rightarrow\Delta ABH\sim\Delta MNO\Rightarrow\dfrac{AH}{OM}=\dfrac{AB}{MN}\)
Mà MN là đường trung bình \(\Rightarrow MN=\dfrac{AB}{2}\Rightarrow\dfrac{AH}{OM}=2\Rightarrow AH=2OM\)
Lại có I là trọng tâm \(\Rightarrow\dfrac{IA}{IM}=2=\dfrac{AH}{OM}\Rightarrow\Delta AHI\sim\Delta MOI\) (hai tam giác có 2 cặp cạnh tương ứng bị lệ và 1 góc đối đỉnh)
\(\Rightarrow\dfrac{IA}{IM}=\dfrac{IH}{OI}=2\Rightarrow IH=2OI\)
Vậy \(\sqrt{\dfrac{OI^2+OM^2}{IH^2+AH^2}}=\sqrt{\dfrac{OI^2+OM^2}{\left(2OI\right)^2+\left(2OM\right)^2}}=\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)

A C B H D M O K
a/ Ta có
\(\widehat{ACK}=90^o\) (góc nội tiếp chắn nửa đường tròn)\(\Rightarrow CK\perp AC\)
\(BH\perp AC\) (BH là đường cao)
=> BH//CK (vì cùng vuông góc với AC) (1)
Ta có
\(\widehat{ABK}=90^o\) (góc nội tiếp chắn nửa đường tròn)\(\Rightarrow BK\perp AB\)
\(CH\perp AB\) (CH là đường cao)
=> CH//BK (cùng vuông góc với AB (2)
Từ (1) và (2) => BHCK là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một thì tứ giác đó là hbh)
b/ Nối BO cắt đường tròn tại D ta có
\(\widehat{BCD}=90^o\) (góc nội tiếp chắn nửa đường tròn)\(\Rightarrow CD\perp BC\)
\(AH\perp BC\) (AH là đường cao)
=> AH//CD (cùng vuông góc với BC) (3)
Ta có
\(\widehat{BAD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AD\perp AB\)
\(CH\perp AB\) (CH là đường cao)
=> AD//CH (cùng vuông góc với AB) (4)
Từ (3) và (4) => AHCD là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một thì tứ giác đó là hbh)
=> AH=CD (trong hbh các cặp cạnh đối bằng nhau từng đôi một)
Xét \(\Delta BCD\) có
\(BM=CM;BO=DO\) => OM là đường trung bình của \(\Delta BCD\Rightarrow OM=\frac{1}{2}CD\)
Mà \(CD=AH\Rightarrow OM=\frac{1}{2}AH\left(dpcm\right)\)

a) chắc đề hỏi là tứ giác BHCD là hình gì chứ ko có điểm K
Vì AD là đường kính \(\Rightarrow\left\{{}\begin{matrix}\angle ACD=90\\\angle ABD=90\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}CD\bot AC\\BD\bot AB\end{matrix}\right.\)
mà \(\left\{{}\begin{matrix}BH\bot AC\\CH\bot AB\end{matrix}\right.\Rightarrow\) \(CD\parallel BH,BD\parallel CH\) \(\Rightarrow BHCD\) là hình bình hành
b) Vì BHCD là hình bình hành có I là trung điểm BC
\(\Rightarrow H,I,D\) thẳng hàng và I cũng là trung điểm HD
Xét \(\Delta AHD\) có O là trung điểm AD,I là trung điểm HD
\(\Rightarrow OI\) là đường trung bình \(\Rightarrow OI=\dfrac{1}{2}AH\Rightarrow AH=2OI\)
c) AI cắt HO tại G'.
Vì \(OI\parallel AH\) \(\Rightarrow\dfrac{AH}{OI}=\dfrac{AG'}{G'I}\Rightarrow\dfrac{AG'}{G'I}=2\Rightarrow\dfrac{AG'}{AI}=\dfrac{2}{3}\)
\(\Rightarrow G'\) là trọng tâm tam giác ABC \(\Rightarrow G\equiv G'\Rightarrow\) đpcm
Vì \(OI\parallel AH\) \(\Rightarrow\dfrac{GH}{GO}=\dfrac{AH}{OI}=2\Rightarrow GH=2GO\)
d) Kẻ \(AF\bot HO\) \(\Rightarrow\left\{{}\begin{matrix}S_{AOG}=\dfrac{1}{2}.AF.OG\\S_{AHG}=\dfrac{1}{2}.AF.HG\end{matrix}\right.\)
mà \(GH=2GO\Rightarrow S_{AHG}=2S_{AOG}\)