Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Do tam giác vuông cân tại A nên AB = AC = a và ![]() và góc C = 450
và góc C = 450
Ta có ![]()

\(\overrightarrow{CA}-\overrightarrow{CB}=\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{BA}\)

Dựng hình hình hành CADB.
A B C D
Theo quy tắc hình bình hành: \(\overrightarrow{CA}+\overrightarrow{CB}=\overrightarrow{CD}\).
Vì vậy \(\left|\overrightarrow{CA}+\overrightarrow{CB}\right|=\left|\overrightarrow{CD}\right|=CD\);
Mặt khác \(\left|\overrightarrow{CA}-\overrightarrow{CB}\right|=\left|\overrightarrow{CA}+\overrightarrow{BC}\right|=\left|\overrightarrow{BA}\right|=BA\).
Suy ra: \(CD=AB\).
Hình bình hành CADB có hai đường chéo bằng nhau (\(CD=AB\) )nên hình bình hành CADB là hình chữ nhật.

A B C A' B' C' I D
\(\overrightarrow{ID}.\overrightarrow{AA'}=\overrightarrow{ID}\left(\overrightarrow{IA'}-\overrightarrow{IA}\right)=\overrightarrow{ID}.\overrightarrow{IA'}-\overrightarrow{ID}.\overrightarrow{IA}=IA'^2-\overrightarrow{ID}.\overrightarrow{IA}\)
\(=IA'^2-\left(\overrightarrow{IC'}+\overrightarrow{C'D}\right)\overrightarrow{IA}=IA'^2-\overrightarrow{IC'}.\overrightarrow{IA'}-\overrightarrow{C'D}.\overrightarrow{IA}=IA'^2-IC'^2-0\) (vì AI vuông góc với C'B')
\(=r^2-r^2=0\) (r là bán kính đường tròn nội tiếp tam giác ABC)
ĐFCM

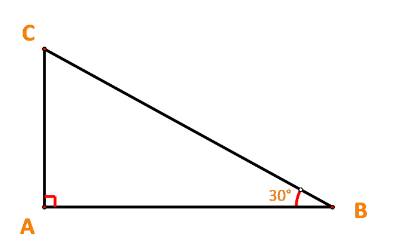
Ta có: \(BC = \frac{{AB}}{{\cos {{30}^o}}} = 3:\frac{{\sqrt 3 }}{2} = 2\sqrt 3 \); \(AC = BC.\sin \widehat {ABC} = 2\sqrt 3 .\sin {30^o} = \sqrt 3 .\)
\(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = 3.2\sqrt 3 .\cos \widehat {ABC} = 6\sqrt 3 .\cos {30^o} = 6\sqrt 3 .\frac{{\sqrt 3 }}{2} = 9.\)
\(\overrightarrow {CA} .\overrightarrow {CB} = \left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {CB} } \right|\cos (\overrightarrow {CA} ,\overrightarrow {CB} ) = \sqrt 3 .2\sqrt 3 .\cos \widehat {ACB} = 6.\cos {60^o} = 6.\frac{1}{2} = 3.\)