Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(AB^2\) = BH . BC ; \(AC^2\) = CH . BC
Ta có:
⇒ BH = 49 . 1 = 49
⇒ CH = 576 . 1 = 576
a) Ta có: \(\dfrac{BH}{HC}=\left(\dfrac{AB}{AC}\right)^2\)
\(\Leftrightarrow\dfrac{BH}{HC}=\dfrac{49}{576}\)
hay \(BH=\dfrac{49}{576}HC\)
Ta có: BH+HC=BC(H nằm giữa B và C)
\(\Leftrightarrow HC\cdot\dfrac{625}{576}=625\)
hay HC=576(cm)
\(\Leftrightarrow HB=BC-BH=625-576=49\left(cm\right)\)

Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. a) Biết AH = 6cm, BH = 4,5cm.Tính AB, AC, BC,HC. b) Biết AB = 6cm, BH = 3cm.Tính AH và tính chu vi của các tam giác vuông trong hình.
Bài 1:
\(HC=\dfrac{AH^2}{HB}=\dfrac{36}{4.5}=8\left(cm\right)\)
BC=BH+CH=12,5cm
\(AB=\sqrt{4.5\cdot12.5}=7.5\left(cm\right)\)
\(AC=\sqrt{8\cdot12.5}=10\left(cm\right)\)

Bài 1) Ta có △ABC có đường cao AH ⇒AH2=BH.HC⇒36=4,5.HC⇒HC=8(cm)
Ta có BC=HC+BH=4,5+8=12,5(cm)
Ta có AB2=BH.BC=4,5.12,5=56,25⇒AB=7,5(cm)
Ta có AC2=BC2-AB2=156,25-56,25=100⇒AC=10(cm)
Bài 2) Chắc bạn ghi sai đề rồi

4. Dễ thấy \(\Delta AML\approx\Delta LKC\left(g-g\right)\)
\(\Rightarrow\frac{AL}{LC}=\sqrt{\frac{S_{\Delta AML}}{S_{\Delta LKC}}}=\sqrt{\frac{42.7283}{51.4231}}\approx0.9115461896\)
\(\Rightarrow\frac{AL}{AC}=\frac{0.9115461896}{0.9115461896+1}=0.476863282\)
Lại có \(\Delta AML\approx\Delta ABC\left(g-g\right)\)
\(\Rightarrow\frac{S_{AML}}{S_{ABC}}=\left(\frac{AL}{AC}\right)^2=0.476863282^2=0.2273985897\)
\(\Rightarrow S_{\Delta ABC}=\frac{S_{\Delta AML}}{0.2273985897}=\frac{42.7283}{0.2273985897}\approx187.9\left(cm^2\right)\)
1. Ta có \(\frac{BH}{CH}=\frac{\sqrt{7}}{\sqrt{5}}\Rightarrow BH=\frac{\sqrt{7}}{\sqrt{5}}CH\)
Mặt khác \(BC=\sqrt{11}\Rightarrow BH+CH=11\)
\(\Rightarrow\frac{\sqrt{7}}{\sqrt{5}}CH+CH=11\)
\(\Leftrightarrow CH=\frac{-55+11\sqrt{35}}{2}\) và \(BH=\frac{77-11\sqrt{35}}{2}\)
Có BH, CH và BC tính đc AB, AC \(\left(AB=\sqrt{BH.BC};AC=\sqrt{CH.BC}\right)\)
Từ đó tính đc chu vi tam giác ABC.
2. Để cj gửi hình qua gmail cho
3. Chỉ còn cách làm từng bước thôi e
\(B=31+\frac{27}{\frac{30127}{2008}}=31+\frac{54216}{30127}=32+\frac{24089}{30127}\)
Để viết liên phân số, ta bấm phím tìm thương và số dư:
(Mỗi số b1, b2, b3, ..., bn-1 chính là thương; số chia của phép chia trước là số bị chia của phép chia sau, còn số dư của phép chia trước là số chia của phép chia sau, nhớ nhá)
- B1: Tìm thương và số dư của 30127 cho 24089, thương là 1, dư 6038, viết \(B=32+\frac{1}{1+...}\)
- B2: Tìm thương và số dư của 24089 cho 6038, thương là 3, dư 5975, viết \(B=32+\frac{1}{1+\frac{1}{3+...}}\)
- B3: Tìm thương và số dư của 6038 cho 5975, thương là 1, dư 63, viết \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+...}}}\)
- B4: Tìm thương và số dư của 5975 cho 63, thương là 94, dư 53, viết \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+\frac{1}{94+...}}}}\)
...
Cứ làm như vậy, đến khi số dư là 1 thì dừng lại, phân số cuối cùng \(\frac{1}{b_n}\) thì bn chính là số chia cuối cùng, bn = 3
Kết quả: \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+\frac{1}{94+\frac{1}{1+\frac{1}{5+\frac{1}{3+\frac{1}{3}}}}}}}}\)

a: \(BC=\sqrt{4.5^2+6^2}=7.5\left(cm\right)\)
AH=4,5*6/7,5=3,6(cm)
BH=AB^2/BC=4,5^2/7,5=2,7cm
CH=7,5-2,7=4,8cm
b: BH/CH=1/4
nên CH=4BH
Ta có; AH^2=HB*HC
=>4HB^2=14^2=196
=>HB=7cm
=>CH=28cm
=>BC=35cm; \(AB=\sqrt{7\cdot35}=7\sqrt{5}\left(cm\right)\)
\(AC=\sqrt{28\cdot35}=14\sqrt{5}\left(cm\right)\)
=>\(C=21\sqrt{5}+35\left(cm\right)\)

Bài này mk chỉ làm đk theo 2 cách thôi nha , tại cách thứ 3 mk quên ko ghi vô vở rồi :
Cách 1 :
Gọi độ dài các cgv là : AB = 3x
AC = 4x
ADĐL pitago vào tam giác vuông ABC , có :
BC2 = AB2 + AC2
1252 = (3x)2 + (4x)2
1252 = 9x2 + 16x2
15625 = 25x2
x2 = 625
=> x = 25
=> AB= 3x = 3 . 25 = 75 cm
AC = 4x = 4 . 25 = 100 cm
ADHT về cgv và đ/c trong tam giác vuông ABC , ta có :
AB2 = BH . BC
752 = BH . 125
BH = 45 cm
Ta có : BC = BH + HC
125 = 25 + HC
HC = 80 cm
Cách 2 :
Ta có : \(\dfrac{AB}{AC}\)= \(\dfrac{3}{4}\)
<=> \(\dfrac{AB}{3}\) = \(\dfrac{AC}{4}\) <=> \(\left(\dfrac{AB}{3}\right)^2\)= \(\left(\dfrac{AC}{4}\right)^2\)
<=> \(\dfrac{AB^2}{9}\)= \(\dfrac{AC^2}{16}\)
<=> \(\dfrac{AB^2+AC^2}{25}\)= \(\dfrac{BC^2}{25}\)
<=> \(\dfrac{125^2}{25}\) = \(\dfrac{15625}{25}\)= 625
Ta có : \(\dfrac{AB^2}{9}\)= \(\dfrac{AC^2}{16}\)= 625
<=> \(\dfrac{AB^2}{9}\)= 625
=> AB2 = 5625
=> AB = 75 cm
<=> \(\dfrac{AC^2}{16}\)= 625
=> AC2 = 10000
=> AC = 100 cm
BH và HC tính tương tự cách 1
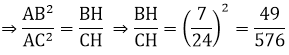
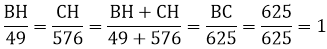

Lời giải:
a. Áp dụng hệ thức lượng trong tam giác vuông:
$AB^2=BH.BC$
$AC^2=CH.CB$
$\Rightarrow (\frac{AB}{AC})^2=\frac{BH.BC}{CH.CB}=\frac{BH}{CH}$
$\Leftrightarrow (\frac{7}{24})^2=\frac{49}{576}=\frac{BH}{CH}$
b.
$\frac{BH}{CH}=\frac{49}{576}$
$BH+CH=BC=625$ (cm)
$\Rightarrow BH=625:(49+576).49=49$ (cm)
$CH=BC-BH=625-49=576$ (cm)
Hình vẽ: