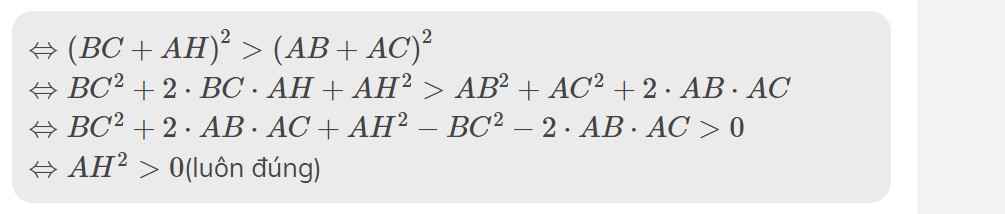H
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VJ
0
20 tháng 2 2016
bài này êm nghĩ một tí là ra mà minh k chịu suy nghĩ nhưng làm ra rùi không cần giúp nữa đâu
KI
2
15 tháng 4 2016
Bạn tự vẽ hình nha.
Ta có : AH.BC=AB.AC ( bằng hai lần diện tích tam giác ABC) nên 2.AH.BC=2.AB.AC(1)
Theo định lí Pi-ta-go, ta có: AC2+AB2=BC2AC2+AB2=BC2(2)
Mà (AH+BC)2=AH2+BC2+2.AH.BC(AH+BC)2=AH2+BC2+2.AH.BC(3)
(AB+AC)2=AB2+AC2+2.AB.AC(AB+AC)2=AB2+AC2+2.AB.AC(4)
Từ (1);(2);(3);(4) suy ra đpcm
15 tháng 4 2016
Bạn tự vẽ hình nha
Ta có: AH.BC=AB.AC⇔2AH.BC=2AB.ACAH.BC=AB.AC⇔2AH.BC=2AB.AC
⇔AB2+2AB.AC+AC2=2AH2+HB2+HC2+2AH.BC⇔AB2+2AB.AC+AC2=2AH2+HB2+HC2+2AH.BC
⇔(AB+AC)2<2HC.HB+HB2+HC2+2AH.BC+AH2=AH2+2AH.BC+BC2=(AH+BC)2⇔(AB+AC)2<2HC.HB+HB2+HC2+2AH.BC+AH2=AH2+2AH.BC+BC2=(AH+BC)2
((AH2=HC.HB)(AH2=HC.HB)
⇒AH+BC>AB+AC
PT
1
16 tháng 6 2022
\(\Leftrightarrow\left(BC+AH\right)^2>\left(AB+AC\right)^2\)
\(\Leftrightarrow BC^2+2\cdot BC\cdot AH+AH^2>AB^2+AC^2+2\cdot AB\cdot AC\)
\(\Leftrightarrow BC^2+2\cdot AB\cdot AC+AH^2-BC^2-2\cdot AB\cdot AC>0\)
\(\Leftrightarrow AH^2>0\)(luôn đúng)
16 tháng 5 2023
a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
AH=AE
=>ΔAHD=ΔAED
b: DH=DE
DE<DC
=>DH<DC
c: Xét ΔAKC có
CH,KE là đường cao
CH căt KE tại D
=>D là trực tâm
=>AD vuông góc KC
FC
1
TA
25 tháng 3 2017
Tam giác ABC vuông tại A nên \(BC^2=AB^2+AC^2\)\(\Rightarrow\)\(BC^2-AB^2-AC^2=0\)
Mặt khác \(2AH.BC=2AB.AC\) (vì cùng bằng diện tích tam giác ABC).
BĐT cần CM tương đương với (AH + BC)2 > (AB + AC)2
hay \(AH^2+BC^2+2AH.BC>AB^2+AC^2+2AB.AC\)
\(\Leftrightarrow\)\(AH^2+\left(BC^2-AB^2-AC^2\right)+\left(2AH.BC-2AB.AC\right)>0\)
\(\Leftrightarrow\)\(AH^2>0\) (luôn đúng).
ND
1
QT
0