Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
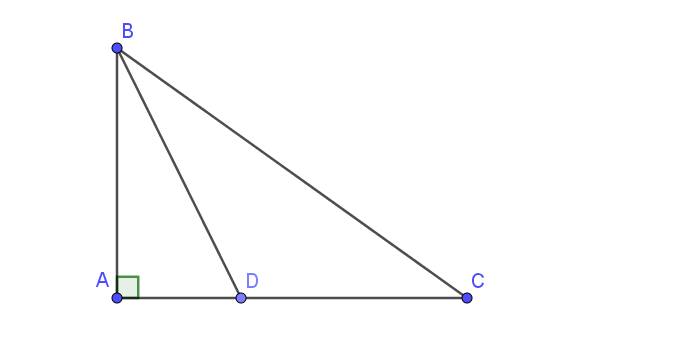
Theo tính chất tia phân giác:
$\frac{AB}{BC}=\frac{AD}{DC}=\frac{4\sqrt{10}}{5\sqrt{10}}=\frac{4}{5}$
$AC=4\sqrt{10}+5\sqrt{10}=9\sqrt{10}$
Áp dụng định lý Viet:
$BC^2=AB^2+AC^2$
$\Leftrightarrow (\frac{5}{4}AB)^2=AB^2+(9\sqrt{10})^2$
$\Leftrightarrow AB^2=1440$
$BD=\sqrt{AB^2+AD^2}=\sqrt{1440+(4\sqrt{10})^2}=\sqrt{1440+160}=40$ (cm)

a, \(vì\)AD là phân giác suy ra góc BAD =góc DAC =45 ĐỘ
cos45 độ = AD/AB =4 /AB =1/ căn 2 suy ra AB =4 NHÂN CĂN 2
TH TỰ dùng sin 45 độ =dc/ac =5/ad =1/căn 2 suy ra AC =5 CĂN 2 ÁP DỤNG PITA GO TÌM RA CẠNH bc
b,

Bạn viết đề sai rồi
Cái \(3\dfrac{14}{17}\) là hỗn số chứ ko phải là số tự nhiên nhân vs phân số
#)Giải :
(Hình bn tự vẽ)
AD là phân giác của ∆ABC \(\Rightarrow\) \(\frac{BD}{AB}=\frac{DC}{AC}\Rightarrow\frac{BD^2}{AB^2}=\frac{DC^2}{AC^2}\)
Ta có : \(BC=BD+CD=3.\frac{14}{17}+9.\frac{3}{17}=\frac{42}{17}+\frac{27}{17}=\frac{69}{17}\)
Mà ∆ABC vuông tại A nên theo định lí Py - ta - go \(\Rightarrow AB^2+AC^2=BC^2\Rightarrow AB^2+AC^2=\left(\frac{69}{17}\right)^2\)
Theo t/chất dãy tỉ số bằng nhau : \(\frac{BD^2}{AB^2}=\frac{DC^2}{AC^2}=\frac{BD^2+DC^2}{AB^2+AC^2}=\frac{\left(\frac{42}{17}\right)^2+\left(\frac{27}{17}\right)^2}{\left(\frac{69}{17}\right)^2}=\) dài dòng vãi ra @@
Chắc đề sai rồi

=) Áp dụng liên tục py-ta-go và định lí đường phân giác quá dễ đó bạn :V
\(\frac{AD}{AB}=\frac{ID}{IB}=\frac{1}{2}vs.AD^2+AB^2=\left(6\sqrt{3}+3\sqrt{3}\right)^2=...\\
\)
Tìm đ.c AD và AB
Làm tươn tự trên đối với tg ABC
\(\frac{AD}{DC}=\frac{AB}{BC}vs.AB^2+\left(AD+DC\right)^2=BC^2.\\
\)
\(Chỉ-cần-giải-hệ-là-ra-....\\
\)

Đặt \(CD=x,BC=y\left(x,y>0\right)\)
Ta có \(AB=\sqrt{BD^2-AD^2}=12\)
Ta có hệ phương trình: \(\hept{\begin{cases}\frac{x}{y}=\frac{AD}{AB}=\frac{4}{12}=\frac{1}{3}\\12^2+\left(4+x\right)^2=y^2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=3x\\144+\left(4+x\right)^2=\left(3x\right)^2\end{cases}}\Leftrightarrow\hept{\begin{cases}y=3x\\x=5\left(h\right)x=-4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=5\\y=15\end{cases}}\)(Vì \(x,y>0\))
Vậy \(S_{ABC}=\frac{AB.\left(AD+CD\right)}{2}=\frac{12.\left(4+5\right)}{2}=54.\)