Question

[Vũ Việt Hà]

Cho tam giác ABC vuông tại A, đường cao AH 

a, Cho biết  HB = 9cm, HC=16 cm. Tính độ dài AH, AB,AC

b, Cm các hệ thức: AH² = HB . HC

                             AB² = BC .BH

Answer 1

[Phúc Nguyễn]

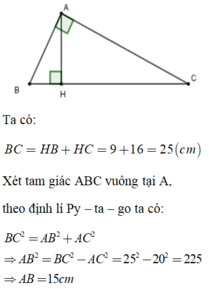
a) \(BC=HC+BH=16+9=25\left(cm\right)\)

Tam giác \(AHC\) và \(AHB\) vuông tại \(H\)

\(\Rightarrow\hept{\begin{cases}AC^2=HC^2+HA^2\\AB^2=AH^2+HB^2\end{cases}}\)

\(\Rightarrow AB^2+AC^2=HC^2+AH^2+AH^2+HB^2\)

\(\Rightarrow BC^2=HC^2+2AH^2+HB^2\)

\(\Rightarrow25^2=16^2+2AH^2+9^2\)

\(\Rightarrow AH=\sqrt{\frac{25^2-16^2-9^2}{2}}=12\)

Trở lại điều kiện ban đầu: \(\hept{\begin{cases}AC^2=HC^2+AH^2\\AB^2=HB^2+HA^2\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}AC=\sqrt{16^2+12^2}=20\\AB=\sqrt{9^2+12^2}=15\end{cases}}\)

b) Khi đã có số đo all cạnh thì cm rất dễ thôi

\(\hept{\begin{cases}AH^2=12^2=144\\HB.HC=16.9=144\end{cases}}\Rightarrowđpcm\)

\(\hept{\begin{cases}AB^2=15^2=225\\BC.HB=9.25=225\end{cases}}\Rightarrowđpcm\)

Answer 2

[Tô Quang Huy]

a ) BC=HC+BH=16+9=25 ( cm )

  Tam giác: AHC và AHB vuông tại H

\(\Rightarrow\hept{\begin{cases}AC^2=HC^2+HA^2\\AB^2=AH^2+HB^2\end{cases}}\)

\(\Rightarrow AB^2+AC^2=HC^2+AH^2+AH^2=HB^2\)

\(\Rightarrow BC^2=HC^2+2AH^2+HB^2\)

\(\Rightarrow25^2=16^2+2AH^2+9^2\)

\(\Rightarrow AH=\sqrt{\frac{25^2-16^2-9^2}{2}=12}\)

Trở lại điều kiện ban đầu:\(\hept{\begin{cases}AC^2=HC^2+AH^2\\AB^2=HB^2+HA^2\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}AC=\sqrt{16^2+12^2=20}\\AB=\sqrt{9^2+12^2=15}\end{cases}}\)

B ) KHI ĐÃ CÓ SỐ ĐO ALL CẠNH THÌ CM RẤT DỄ LÀM THÔI:

\(\hept{\begin{cases}AH^2=12^2=144\\HB.HC=16.9=144\end{cases}}=đpcm\)

\(\hept{\begin{cases}AB^2=15^2=225\\BC.HB=9.25=225\end{cases}}=đpcm\)