Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nha
a)Ta có : BM=BA-AM=30-20=10(cm)
Diện tích tam giác BCM là
S=\(\frac{BM.AC}{2}\)=\(\frac{10.36}{2}\)=180\(cm^2\)
b) Mình làm theo Dịnh lí Ta- lét trong tam giác ABC có MN//BC có:
\(\frac{AM}{AB}=\frac{AN}{AC}\)
<=>\(\frac{20}{30}=\frac{AN}{36}\)
<=>AN=24(cm)
Tứ đó ta có Sbcnm=Sbac-Samn=\(\frac{30.36}{2}\)-\(\frac{24.20}{2}\)=540-240=300(\(cm^2\))

B1:
Diện tích tam giác ABC là:
54 × 60 : 2 = 1620 ( m2 )
Nối A với N ta được tam giác ANC có chiều cao là 10cm và đáy AC là 54cm
Diện tích tam giác ANC là :
10 × 54 : 2 = 270 ( m2 )
Diện tích tam giác ABN là:
1620 - 270 = 1350 ( m2 )
Độ dài đoạn MN là:
1350 × 2 : 60 = 45 ( m)
Vậy đoạn MN dài 45m

Lời giải:
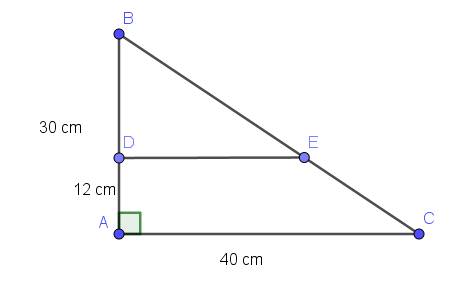
$BD=AB-DA=30-12=18$ (cm)
Diện tích tam giác ABC:
$AB.AC:2=30.40:2=600$ (cm2)
Diện tích tam giác ABC cũng bằng;
$S_{BDE}+S_{ADEC}=BD.DE:2+(DE+AC).AD:2$
$=18.DE:2+(DE+40).12:2$
$=9DE+6(DE+40)$ (cm2)
Vậy: $600=9DE+6(DE+40)=15DE+240$
$\Rightarrow DE=(600-240):15=24$ (cm)
Diện tích hình thang DECA:
$(DE+AC).DA:2=(24+40).12:2=384$ (cm2)

10cm 40cm D A B C E 50cm
Nối \(AE\), tam giác \(EAC\) có chiều cao bằng độ dài đoạn \(AD=10cm\).
Diện tích tam giác \(EAC\) bằng:
\(\frac{50\times10}{2}=250\left(cm^2\right)\)
Diện tích tam giác \(ABC\) bằng:
\(\frac{50\times40}{2}=1000\left(cm^2\right)\)
Diện tích tam giác \(BAE\) ( bằng diện tích tam giác \(ABC\) trừ đi diện tích tam giác \(EAC\) ):
\(1000-250=750\left(cm^2\right)\)
Chiều cao \(ED\) của tam giác \(BAE\) bằng:
\(\frac{750\times2}{40}=37,5\left(cm\right)\)
Độ dài cạnh \(BC\) bằng:
\(50-10=40\left(cm\right)\)
Vì \(DE\) song song với \(AC\) nên \(DE\) vuông góc với \(BD\). Vậy tam giác \(BDE\) là tam giác vuông tại \(D\) và có diện tích bằng:
\(\frac{40\times37,5}{2}=750\left(cm^2\right)\)
Đáp số: \(750cm^2\)
B A D C E 40cm 10cm 50cm
\(S\) \(ABC:\frac{40\times50}{2}=1000\left(cm^2\right)\)
\(S\) \(AEC:\frac{50\times10}{2}=250\left(cm^2\right)\)
\(S\) \(ABE:1000-250=750\left(cm^2\right)\)
\(DE:\frac{750\times2}{40}=37,5\left(cm\right)\)
\(S\) \(BDE:\frac{37,5\times30}{2}=562,5\left(cm^2\right)\)