Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Diện tích ABC = 30 x 40 : 2 = 600 cm2 . Diện tích CEB = 1/2 CB x 12 = 1/2 x 50 x 12 = 300 cm2 .
=> Diện tích tam giác ACE = diện tích ABC - Diện tích CEB = 600 - 300 = 300 cm2
Theo công thức: Diện tích ACE = 1/2 AE x AC = 1/2 AE x 30
Suy ra: 1/2 AE x 30 = 300 => AE = 300 x 2 : 30 = 20 cm.
Tương tự, Diện tích BFC = 300, diện tích AFB = 600 - 300 = 300 => 1/2 AF x AB = 300 => AF = 300 x 2 : 40 = 15 cm
a) Diện tích AEF = 1/2 AF x AE = 1/2 x 20 x 15 = 150 cm2
b) Diên tích EFBC = diện tích ABC - diện tích AEF = 600 - 150 = 450 cm2
Vậy................

MDAC là hình thang có chiều cao 10cm
=>MD//AC và AD=10cm
DB+AD=AB
=>DB+10=30
=>DB=20(cm)
Xét ΔBAC có MD//AC
nên \(\dfrac{MD}{AC}=\dfrac{BD}{BA}\)
=>\(\dfrac{MD}{60}=\dfrac{20}{30}=\dfrac{2}{3}\)
=>\(MD=60\cdot\dfrac{2}{3}=40\left(cm\right)\)
Diện tích hình thang ADMC là:
\(S_{ADMC}=\dfrac{1}{2}\cdot AD\cdot\left(MD+AC\right)\)
\(=\dfrac{1}{2}\cdot10\cdot\left(60+40\right)=5\cdot100=500\left(cm^2\right)\)
Diện tích tam giác ABC là:
\(S_{ACB}=\dfrac{1}{2}\cdot AB\cdot AC=900\left(cm^2\right)\)
\(S_{ABC}=S_{BMD}+S_{CMDA}\)
=>\(S_{BMD}+500=900\)
=>\(S_{DMB}=400\left(cm^2\right)\)
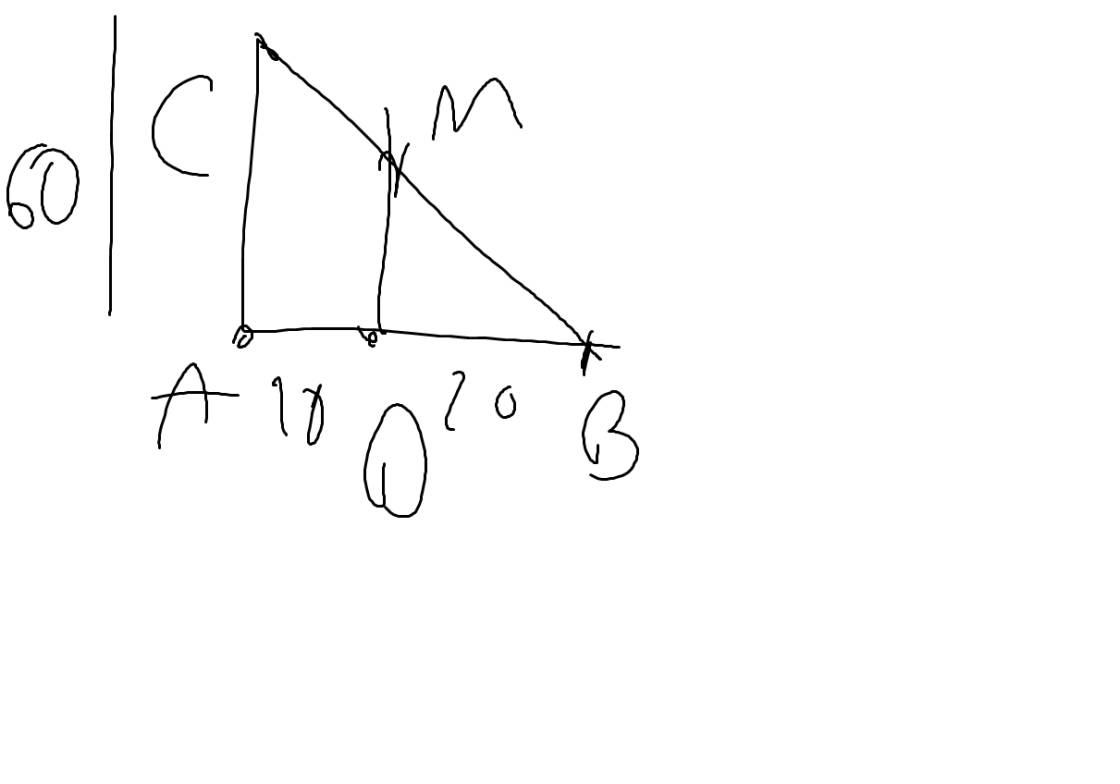
Lời giải:
$BD=AB-DA=30-12=18$ (cm)
Diện tích tam giác ABC:
$AB.AC:2=30.40:2=600$ (cm2)
Diện tích tam giác ABC cũng bằng;
$S_{BDE}+S_{ADEC}=BD.DE:2+(DE+AC).AD:2$
$=18.DE:2+(DE+40).12:2$
$=9DE+6(DE+40)$ (cm2)
Vậy: $600=9DE+6(DE+40)=15DE+240$
$\Rightarrow DE=(600-240):15=24$ (cm)
Diện tích hình thang DECA:
$(DE+AC).DA:2=(24+40).12:2=384$ (cm2)
Hình vẽ: