Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích các bước giải:
BE ⊥ AM, CF⊥AM
=> BE // CF
a) Xét Δ vuông BME và Δ vuông CMF có:
BM = MC ( M là tđ BC )
B1 = C1 ( so le trong )
=> Δ ... = Δ ... ( ch - gn)
b) ME = MF ( cạnh tương ứng )
c) Xét Δ MEC và Δ MFB có:
M1 = M2 (đối đỉnh)
ME = MF (cmt)
BM = CM (cmt)
=> Δ ... = Δ ... ( cgc )
=> CE = BF
d)
Ta có: C2 = B2 (Δ MEC = Δ MFB)
Mà 2 góc này ở vị trí so le trong
=> CE // BF

\(\Delta BEM=\Delta CFM\text{(cạnh huyền - góc nhọn) }\Rightarrow BE=CF\)

a: Xét ΔBME vuông tại E và ΔCMF vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)
Do đó: ΔBME=ΔCMF
Suy ra: BE=CF

Xét 2 TG vuông BME và CMF, ta có:
BM=CM(M là tđiểm BC); BME=CMF(2 góc đđ)
=>TG BME=TG CMF(cạnh huyền-góc nhọn)
=>BE=CF(2 cạnh tương ứng)
Xét 2 TG vuông BME và CMF, ta có:
BM=CM(M là tđiểm BC); BME=CMF(2 góc đđ)
=>TG BME=TG CMF(cạnh huyền-góc nhọn)
=>BE=CF(2 cạnh tương ứng)

câu sai nha bạn người ta bảo điều kiện của tam giác abc chứ ko phải thay canh BE với CE nha

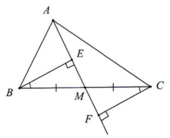
a) xét ΔBME và ΔCMF có :
\(\widehat{BEM}\) = \(\widehat{CFM}\) ( = 90\(^O\))
BM = CM ( M là trung điểm của BC )
\(\widehat{BME}\) = \(\widehat{CMF}\) ( hai góc đối đỉnh )
\(\Rightarrow\) ΔBME = ΔCMF ( cạnh huyền - góc nhọn )
b) ΔBME = ΔCMF (cmt)
\(\Rightarrow\) BE = CF ( hai cạnh tương ứng )