Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

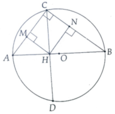
a, Tính được HA=4cm; HB=9cm
b, Tính được HA=4cm; HB=9cm
c, Tính được HM = 12 13 13 cm, HN = 18 13 13 cm
Từ đó tính được S C M H N = 216 13 c m 2

1: góc ACB=1/2*sđ cungAB=90 độ
góc CMH=góc CNH=1/2*sđ cung CH=90 độ
góc CMH=góc CNH=góc MCN=90 độ
=>CMHN là hình chữ nhật
2: CMHN là hình chữ nhật
=>góc CMN=góc CHN=góc CBH
=>góc AMN+góc ABN=180 độ
=>AMNB nội tiếp

a: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
Xét tứ giác CMHN có \(\widehat{CMH}=\widehat{CNH}=\widehat{MCN}=90^0\)
nên CMHN là hình chữ nhật
b: Gọi I là trung điểm của BH
=>I là tâm của đường tròn đường kính BH
ΔHNB vuông tại N
=>N nằm trên đường tròn đường kính BH
=>N nằm trên (I)
=>IH=IN
=>\(\widehat{IHN}=\widehat{INH}\)
mà \(\widehat{IHN}=\widehat{BAC}\)(hai góc đồng vị, HN//AC)
nên \(\widehat{INH}=\widehat{BAC}\)
CMHN là hình chữ nhật
=>\(\widehat{MCH}=\widehat{MNH}\)
=>\(\widehat{MNH}=\widehat{ACH}\)
\(\widehat{INM}=\widehat{INH}+\widehat{MNH}\)
\(=\widehat{BAC}+\widehat{ACH}=90^0\)
=>MN là tiếp tuyến của (I)
hay MN là tiếp tuyến của đường tròn đường kính BH
d: ΔCHO vuông tại H
=>CH<=CO
mà CH=MN
nên MN<=CO
Dấu '=' xảy ra khi H trùng với O
=>CO\(\perp\)AB tại O
Xét ΔCAB có
CO là đường trung tuyến
CO là đường cao
Do đó; ΔCAB cân tại C
Xét ΔCAB cân tại C có \(\widehat{ACB}=90^0\)
nên ΔCAB vuông cân tại C
=>\(\stackrel\frown{CA}=\stackrel\frown{CB}\)
=>C là điểm chính giữa của cung AB

a)Ta có:
AO=OB=OD = 13:2=7,5 cm
Theo Py-ta-go suy ra:\(OH=\sqrt{7,5^2-6^2}=4,5cm\)
Do đó:
AH = AO-OH = 7,5-4,5 = 3 cm
HB = OH + OB = 4,5+7,5 = 12 cm
b)Dễ thấy tứ giác CMHN là hcn (do có 3 góc vuông)
Ta có:
+Theo Py-ta-go: \(AC=\sqrt{AH^2+HC^2}=3\sqrt{5}cm\)
+Hệ thức lượng trong tam giác:\(CH^2=CM.AC\)suy ra \(CM=\frac{12\sqrt{5}}{5}cm\)
+Hệ thức lượng trong tam giác:\(\frac{1}{MH^2}=\frac{1}{AH^2}+\frac{1}{CH^2}\)
Suy ra \(MH=\frac{6\sqrt{5}}{5}cm\)
Vậy S(CMHN) = CM.MH = 14,4 CM^2

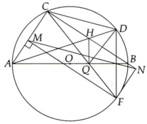
a, Tứ giác BDQH nội tiếp vì B D H ^ + B Q H ^ = 180 0
b, Vì tứ giác ACHQ nội tiếp =>
C
A
H
^
=
C
Q
H
^
Vì tứ giác ACDF nội tiếp => C A D ^ = C F D ^
Từ đó có C Q H ^ = C F D ^ mà 2 góc ở vị trí đồng vị => DF//HQ
c, Ta có H Q D ^ = H B D ^ (câu a)
H B D ^ = C A D ^ = 1 2 s đ C D ⏜
C A D ^ = C Q H ^ (ACHQ cũng nội tiếp)
=>
H
Q
D
^
=
H
Q
C
^
=> QH là phân giác
C
Q
D
^
Mặt khác chứng minh được CH là phân giác góc Q C D ^
Trong tam giác QCD có H là giao của ba đường phân giác nên H là tâm đường tròn nội tiếp => H cách đều 3 cạnh CD, CQ, DQ
d, Vì CMFN là hình chữ nhật nên MN và CF cắt nhau tại trung điểm của mỗi đường.
Trong tam giác FCD có MN//CD và MN đi qua trung điểm CF nên MN đi qua trung điểm DF
Mặt khác AB đi qua trung điểm của DF nên 3 đường thẳng MN, AB, DF đồng quy
bạn giải thích lại giúp mình câu b được không ạ? tại mình không hiểu câu đó lắm, mình cảm ơn!