Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

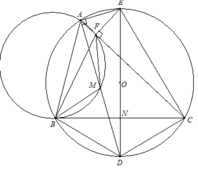
2). Từ AD là phân giác B A C ^ suy ra DB=DC vậy DE vuông góc với BC tại trung điểm N của BC.
Từ 1). Δ B D M ∽ Δ B C F , ta có D M C F = B D B C .
Vậy ta có biến đổi sau D A C F = 2 D M C F = 2 B D B C = C D C N = D E C E (3).
Ta lại có góc nội tiếp A D E ^ = F C E ^ (4).
Từ 3 và 4, suy ra Δ E A D ∽ Δ E F C ⇒ E F C ^ = E A D ^ = 90 ° ⇒ E F ⊥ A C

\(\Delta CIM=\Delta AIN\left(c.g.c\right)\Rightarrow AN=MC\).
\(\Delta CIN=\Delta AIM\left(c.g.c\right)\)\(\Rightarrow NC=MA\).
Tam giác ABC vuông tại A có AM là đường trung tuyến nên CM = AM = MB.
Vì vậy NC = NA = AM = MC hay tứ giác NCMA là hình thoi, suy ra CA vuông góc với MN
Có IN = IM và MN vuông góc với CA nên M đối xứng với N qua AC.

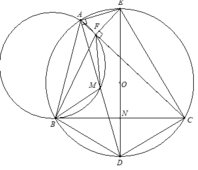
1). Ta có góc nội tiếp bằng nhau B D M ^ = B C F ^ ( 1 ) và B M A ^ = B F A ^ suy ra 180 0 − B M A ^ = 180 0 − B F A ^ hay B M D ^ = B F C ^ (2).
Từ (1) và (2), suy ra Δ B D M ~ Δ B C F (g - g).

\(\overrightarrow{OA'}+\overrightarrow{OB'}+\overrightarrow{OC'}\)
\(=\overrightarrow{OA}+\overrightarrow{AA'}+\overrightarrow{OB}+\overrightarrow{BB'}+\overrightarrow{OC}+\overrightarrow{CC'}\)
\(=\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)+\left(\overrightarrow{BA}+\overrightarrow{CB}+\overrightarrow{AC}\right)\)
\(=\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)+\overrightarrow{CC}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\) (đpcm)

Bẹn tự vẽ hình nhé
Vì A' đối xứng với B qua A => AA' =AB
=. \(\overrightarrow{A'A}=\overrightarrow{AB}\)
Vì B' đối xứng với C qua B => \(\overrightarrow{B'B}=\overrightarrow{BC}\)
Vì C' đối xứng với A qua C => \(\overrightarrow{C'C}=\overrightarrow{CA}\)
Ta có: \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\left(\overrightarrow{OA'}+\overrightarrow{A'A}\right)+\left(\overrightarrow{OB'}+\overrightarrow{B'B}\right)+\left(\overrightarrow{OC'}+\overrightarrow{C'C}\right)\)
\(=\left(\overrightarrow{OA'}+\overrightarrow{OB'}+\overrightarrow{OC'}\right)+\left(\overrightarrow{A'A}+\overrightarrow{B'B}+\overrightarrow{C'C}\right)\)
Lại có: \(\overrightarrow{A'A}+\overrightarrow{B'B}+\overrightarrow{C'C}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}\)\(=\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{CA}=\overrightarrow{AC}+\overrightarrow{CA}=\overrightarrow{AC}-\overrightarrow{AC}=0\)
\(\Rightarrow\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OA'}+\overrightarrow{OB'}+\overrightarrow{OC'}+0=\overrightarrow{OA'}+\overrightarrow{OB'}+\overrightarrow{OC'}\)

a,vì N là trung điểm AC nên 2BN=BA+BC ta có
MA+NB+PC=1/2BA+1/2BC+NB=1/2 (BA+BC)+NB=1/2×2×BN+NB=BN+NB=0 (TM đề bài )
b, vì M;N;P làtrung điểm AB;AC;BC
2OM+2ON+2OP=OA+OB+OA+OC+OB+OC
=2OA+2OB+2OC
suy ra OM+ON+OP=OA+OB+OC
c,
Cm tương tự
2OB=OB'+OC
2OA=OA'+OB
2OC=OA+OC'
suy ra
2OA+2OB+2OC=OA+OB+OC+OA'+OB'+OC'
suy ra OA+OB+OC=OA'+OB'+OC'
