Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi D,E,F lần lượt là tiếp điểm của (I;r) với MN,PQ,RS; T,U,V lần lượt là tiếp điểm của (I;r) với BC,AC,AB
Xét đường tròn (I;r) có hai tiếp tuyến tại D và U cắt nhau tại M \(\Rightarrow MD=MU\)(tính chất hai tiếp tuyến cắt nhau)
Tương tự, ta cũng có: \(SU=SF;\)\(RF=RT;\)\(QT=QE;\)\(PE=PV;\)\(NV=ND\)
Mà \(P_1=AM+AN+MN=AM+AN+MD+ND=AM+AN+MU+NV\)(1)
\(P_2=BP+BQ+PQ=BP+BQ+PE+QE=BP+BQ+PV+QT\)(2)
\(P_3=CS+CR+SR=CS+CR+SF+RF=CS+SR+RT+SU\)(3)
Từ (1), (2) và (3) \(\Rightarrow P_1+P_2+P_3=AM+AN+MU+NV+BP+BQ+PV+QT+CS+CR+RT+SU\)
\(=AM+AN+BP+BQ+CS+CR+\left(MU+SU\right)+\left(RT+QT\right)+\left(PV+NV\right)\)
\(=AM+AN+BP+BQ+CS+CR+MS+RQ+NP\)
\(=\left(AM+CS+MS\right)+\left(AN+BP+NP\right)+\left(BQ+QR+RC\right)\)
\(=AC+AB+BC=P\)
Vậy đẳng thức được chứng minh

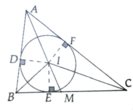
a, Áp dụng tính chất 2 tiếp tuyến tại A,B,C ta chứng minh được b + c - a 2 = AD
b, S A B C = S A I B + S B I C + S C I A
Mà ID = IE = IF = r => S A B C = p.r
c, Vì AM là phân giác của
B
A
C
^
=>
B
M
M
C
=
B
A
A
C
Áp dụng tính chất tỉ lệ thức thu được BM = a c c + b

Đoạn thẳng f: Đoạn thẳng [B, C] Đoạn thẳng h: Đoạn thẳng [B, A] Đoạn thẳng i: Đoạn thẳng [C, A] Đoạn thẳng k_1: Đoạn thẳng [X, Y] Đoạn thẳng n: Đoạn thẳng [B, Y] Đoạn thẳng p: Đoạn thẳng [E, A] Đoạn thẳng q: Đoạn thẳng [E, I] Đoạn thẳng r: Đoạn thẳng [Y, K] Đoạn thẳng s: Đoạn thẳng [N, I] Đoạn thẳng a: Đoạn thẳng [I, M] Đoạn thẳng b: Đoạn thẳng [E, M] Đoạn thẳng c: Đoạn thẳng [A, I] Đoạn thẳng d: Đoạn thẳng [N, M] B = (-1.6, -0.66) B = (-1.6, -0.66) B = (-1.6, -0.66) C = (5.82, -0.68) C = (5.82, -0.68) C = (5.82, -0.68) Điểm A: Điểm trên g Điểm A: Điểm trên g Điểm A: Điểm trên g Điểm X: Điểm trên f Điểm X: Điểm trên f Điểm X: Điểm trên f Điểm Y: Giao điểm đường của j, i Điểm Y: Giao điểm đường của j, i Điểm Y: Giao điểm đường của j, i Điểm I: Giao điểm đường của l, m Điểm I: Giao điểm đường của l, m Điểm I: Giao điểm đường của l, m Điểm E: Trung điểm của n Điểm E: Trung điểm của n Điểm E: Trung điểm của n Điểm K: Giao điểm đường của l, f Điểm K: Giao điểm đường của l, f Điểm K: Giao điểm đường của l, f Điểm N: Giao điểm đường của m, i Điểm N: Giao điểm đường của m, i Điểm N: Giao điểm đường của m, i Điểm M: Giao điểm đường của t, k_1 Điểm M: Giao điểm đường của t, k_1 Điểm M: Giao điểm đường của t, k_1 K
Gọi trung điểm của XY, YC và BC lần lượt là M, N và K..
Do I là tâm đường tròn ngoại tiếp tam giác XYC nên \(\widehat{YMI}=\widehat{YNI}=90^o\)
Vậy ta có YMIN là tứ giác nội tiếp hay \(\widehat{IYN}=\widehat{IMN}\Rightarrow\widehat{AYI}=\widehat{EMI}\) (1)
Xét tam giác BYX có E và M lần lượt là trung điểm của YB và YX nên EM song song và bằng một nửa BX.
Ta cũng có ngay E, M, N thẳng hàng.
Do XY // AB nên \(\frac{AY}{AC}=\frac{BX}{BC}\Rightarrow\frac{AY}{BX}=\frac{AC}{BC}\)
\(\Rightarrow\frac{AY}{EM}=\frac{AY}{\frac{BX}{2}}=2.\frac{AY}{BX}=\frac{2.AC}{BC}=\frac{AC}{BK}\)'
Do tam giác ABC cân tại A nên \(AK\perp BC\)
Xét tam giác vuông ABK, theo định nghĩa tỉ số lượng giác thì \(cos\widehat{ABC}=\frac{BK}{AB}\)
Vậy thì \(\frac{YI}{MI}=\frac{1}{sin\widehat{XYK}}=\frac{1}{cos\widehat{YXK}}=\frac{1}{cos\widehat{ABC}}=\frac{1}{\frac{BK}{AB}}=\frac{AB}{BK}=\frac{AC}{BK}\)
Vậy nên \(\frac{AY}{EM}=\frac{YI}{MI}\) (2)
Từ (1) và (2) ta có \(\Delta AYI\sim\Delta EMI\left(c-g-c\right)\Rightarrow\widehat{IEN}=\widehat{IAN}\)
Xét tứ giác AEIN có \(\widehat{IEN}=\widehat{IAN}\) nên nó là tứ giác nội tiếp.
\(\Rightarrow\widehat{AEI}=180^o-\widehat{ANI}=90^o\)
mình xin sửa lại yêu cầu là: chứng minh góc AEI bằng 90
mong các bạn giúp