Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AHIK có
\(\widehat{AHI}+\widehat{AKI}=90^0+90^0=180^0\)
=>AHIK là tứ giác nội tiếp
=>A,H,I,K cùng thuộc một đường tròn
b: Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó ΔACD vuông tại C
=>AC\(\perp\)CD
Ta có: BH\(\perp\)AC
AC\(\perp\)CD
Do đó:BH//CD
c: Ta có: BH//CD
I\(\in\)BH
Do đó: BI//CD
Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó; ΔABD vuông tại B
Ta có:BD\(\perp\)BA
CI\(\perp\)BA
Do đó:BD//CI
Xét tứ giác BICD có
BI//CD
BD//CI
Do đó: BICD là hình bình hành

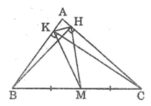
Gọi M là trung điểm của BC.
Tam giác BCH vuông tại H có HM là đường trung tuyến nên:
HM = (1/2).BC (tính chất tam giác vuông)
Tam giác BCK vuông tại K có KM là đường trung tuyến nên:
KM = (1/2).BC (tính chất tam giác vuông)
Suy ra: MB = MC = MH = MK
Vậy bốn điểm B, C, H, K cùng nằm trên một đường tròn tâm M bán kính bằng (1/2).BC.

a) Xét tứ giác BIKC có
\(\widehat{BIC}=\widehat{BKC}\left(=90^0\right)\)
nên BIKC là tứ giác nội tiếp
hay B,I,K,C cùng thuộc đường tròn đường kính BC(Vì \(\widehat{BIC}=\widehat{BKC}=90^0\))
b) Xét tứ giác AIHK có
\(\widehat{AIH}+\widehat{AKH}=180^0\)
nên AIHK là tứ giác nội tiếp
hay A,I,H,K cùng thuộc 1 đường tròn

Lời giải:
1.
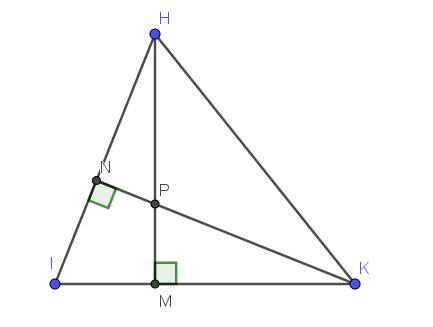
Xét tứ giác $HNMK$ có $\widehat{HNK}=\widehat{HMK}=90^0$. Mà 2 góc này cùng nhìn cạnh $HK$ nên $HNMK$ là tứ giác nội tiếp.
$\Rightarrow H,N,M,K$ cùng thuộc 1 đường tròn.
2.
Xét tứ giác $INPM$ có tổng 2 góc đối nhau $\widehat{INP}+\widehat{IMP}=90^0+90^0=180^0$ nên $INPM$ là tứ giác nội tiếp.
$\Rightarrow I,N, P,M$ cùng thuộc 1 đường tròn.

1: Xét tứ giác HNMK có
\(\widehat{HNK}=\widehat{HMK}=90^0\)
=>HNMK là tứ giác nội tiếp đường tròn đường kính HK
=>H,N,M,K cùng thuộc 1 đường tròn
2: Xét tứ giác INPM có
\(\widehat{INP}+\widehat{IMP}=90^0+90^0=180^0\)
=>INPM là tứ giác nội tiếp
=>I,N,P,M cùng thuộc 1 đường tròn