Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔBHA vuông tại H
=>BH<AB
ΔCKA vuông tại K
=>CK<AC
=>BH+CK<AB+AC
b: ΔBDH vuông tại H
=>BH<BD
ΔCKD vuông tại K
=>CK<CD
=>BH+CK<BD+CD=BC

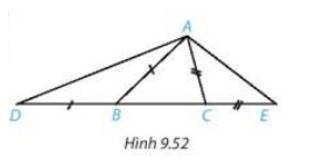
a, vì CA=CE(GT) =>TAM GIÁC ACE CÂN TẠI C=> GÓC CAE= GÓC AEC
b,vì AB<AC=>góc ABC>góc ACB(quan hệ giữa góc và cạnh trong 1 tam giác)
c, vì AH là đường cao => AH là đường vuông góc
TA CÓ AB=BD, AC=CE MÀ AB<AC=>BD<CE=>HD<HE(quan hệ giữa đx và hc)

a)
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).

a: góc C=90-60=30 độ
góc B>góc C
=>AC>AB
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
HC chung
HA=HD
=>ΔAHC=ΔDHC
c: ΔAHC=ΔDHC
=>CA=CD
mà HA=HD
nên CH là trung trực của AD
=>BC là trung trực của AD

a: Xét ΔABD có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABD cân tại A
=>AB=AD
b: Ta có: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}+30^0=90^0\)
=>\(\widehat{ABC}=60^0\)
Xét ΔABD cân tại A có \(\widehat{ABD}=60^0\)
nên ΔABD đều
c: Ta có: ΔABD đều
=>\(\widehat{BAD}=60^0\)
Ta có: \(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\)
=>\(\widehat{CAD}=90^0-60^0=30^0\)
Xét ΔDAC có \(\widehat{DAC}=\widehat{DCA}\left(=30^0\right)\)
nên ΔDAC cân tại D
=>DA=DC
Xét ΔDHA vuông tại H và ΔDEC vuông tại E có
DA=DC
\(\widehat{ADH}=\widehat{CDE}\)(hai góc đối đỉnh)
Do đó: ΔDHA=ΔDEC
=>AH=EC
d: Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}\)
=>\(\dfrac{5}{BC}=sin30=\dfrac{1}{2}\)
=>\(BC=5\cdot2=10\left(cm\right)\)
Xét ΔAHB vuông tại H có \(sinB=\dfrac{AH}{AB}\)
=>\(\dfrac{AH}{5}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(AH=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)