Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, tứ giác AHCE là hình chữ nhật , vì AD=DC và HD=DE
b, áp dụng đl pytago vào tam giác vuông AHC( H là đường cao ABC):
\(HC^2=AC^2-AH^2\\ HC^2=10^2-6^2\\ HC=\sqrt{10^2-6^2}=8cm\)
\(S_{AHCE}=AH.HC=6.8=48cm^2\)

a: Xét tứ giác AHCE có
D là trung điểm chung của AC và HE
góc AHC=90 độ
Do đó: AHCE là hình chữ nhật
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
=>BC=2*BH=6cm
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot4=2\cdot6=12\left(cm^2\right)\)

a: Xét tứ giác AHCD có
I là trung điểm chung của AC và HD
=>AHCD là hình bình hành
Hình bình hành AHCD có \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
b: Ta có: AHCD là hình chữ nhật
=>\(AC^2=AD^2+AH^2\)
=>\(AC^2=6^2+8^2=100\)
=>\(AC=\sqrt{100}=10\left(cm\right)\)
Ta có: ΔAHC vuông tại H
mà HI là đường trung tuyến
nên \(HI=\dfrac{AC}{2}=5\left(cm\right)\)


Bài giải:
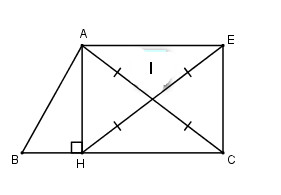
Theo giả thiết II là trung điểm của ACAC nên IA=ICIA=IC
EE là điểm đối xứng với HH qua II nên II là trung điểm của HEHE hay IE=IHIE=IH
Tứ giác AHCEAHCE có hai đường chéo cắt nhau tại trung điểm mỗi đường do đó là hình bình hành (theo dấu hiệu nhận biết 4)
Mặt khác AHAH là đường cao nên ˆAHC=900AHC^=900
Do đó AHCEAHCE là hình chữ nhật (theo dấu hiệu nhận biết 3)
giác AHCE là hình gì ? Vì sao ?
Bài giải:
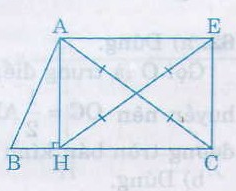
Ta có IA = IC (gt)
IE = IH (gt)
Nên AHCE là hình bình hành (dấu hiệu nhận biết 4)
Lại có ˆAHCAHC^ =1v
Nên AHCE là hình chữ nhật (dấu hiệu nhận biết 3) (Hoặc hình bình hành AHCE là hình chữ nhật vì có hai đường chéo bằng nhau).

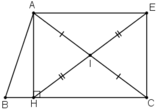
I là trung điểm của AC ⇒ IA = IC.
E đối xứng với H qua I ⇒ IE = IH
⇒ AC ∩ HE = I là trung điểm của AC và HE
⇒ AHCE là hình bình hành (dấu hiệu nhận biết 4)
Lại có : Ĥ = 90º
⇒ AHCE là hình chữ nhật (đpcm).

a) Để chứng minh tam giác ABC vuông, ta cần chứng minh rằng tổng bình phương hai cạnh góc nhọn bằng bình phương cạnh huyền.
Áp dụng định lý Pythagoras, ta có:
AB^2 + AC^2 = 6^2 + 8^2 = 36 + 64 = 100
BC^2 = 10^2 = 100
Vậy AB^2 + AC^2 = BC^2, từ đó ta có thể kết luận rằng tam giác ABC là tam giác vuông tại góc A.
b) Ta có:
- H là chân đường cao từ A xuống BC, nên AH là đường cao của tam giác ABC.
- D là điểm đối xứng với H qua AB, nên AD = AH.
- M là giao điểm của AB và HD, nên AM là trung tuyến của tam giác AHD, do đó AM = MD.
- E là điểm đối xứng với H qua AC, nên AE = AH.
- N là giao điểm của AC và HE, nên AN là trung tuyến của tam giác AHE, do đó AN = NE.
Từ đó, ta có AH = AD = AE và AM = MD, AN = NE.
Vậy ta có thể kết luận rằng AH = MN.
c) Để chứng minh D đối xứng với E qua A, ta cần chứng minh rằng AD = AE và góc DAE = 180 độ.
Ta đã chứng minh trong phần b) rằng AD = AE.
Để chứng minh góc DAE = 180 độ, ta cần chứng minh rằng góc DAB + góc BAE = 180 độ.
Vì tam giác ABC là tam giác vuông tại A (chứng minh trong phần a)), nên góc DAB + góc BAE = 90 độ + 90 độ = 180 độ.
Từ đó, ta có thể kết luận rằng D đối xứng với E qua A.
Đồng thời, F là trung điểm BC, nên AF song song với HD (do D là điểm đối xứng với H qua AB) và AF song song với HE (do E là điểm đối xứng với H qua AC).
Vậy ta có thể kết luận rằng AF vuông góc với MN.

Xét tứ giác AHCE có
D là trung điểm của AC
D là trung điểm của HE
Do đó: AHCE là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật
\(S_{AHCE}=AH\cdot HC=6\cdot8=48\left(cm^2\right)\)