Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H
trong tam giac AHC co \(AH=AC\cdot\sin C=35\cdot\sin50\approx26,8\)
ap dung dl pitago vao AHC ta tinh dc \(HC=AC^2-AH^2\approx22,5\)
tg tu trong tam giac ABH co \(BH=\cot60\cdot26,8\approx15,5\)
\(\Rightarrow BC=BH+CH=38\)
\(\Rightarrow SABC=\frac{1}{2}BC\cdot AH=509,2\)

Bài 2:
\(\cos60^0=\dfrac{28^2+35^2-BC^2}{2\cdot28\cdot35}\)
\(\Leftrightarrow2009-BC^2=980\)
hay \(BC=7\sqrt{21}\left(cm\right)\)

a) Trong tam giác vuông BCH, ta có:
CH=BC.sinB^=12.sin60≈10,392 (cm)
Trong tam giác vuông ABC, ta có:
\(A\)=180−(60+40)=80
Trong tam giác vuông ACH, ta có:
\(AC=\dfrac{CH}{sinA}=\dfrac{10,932}{sin80}=10,552\left(cm\right)\)
b) Kẻ AK⊥BCAK⊥BC
Trong tam giác vuông ACK, ta có:
AK=AC.sinC≈10,552.sin40=6,783 (cm)
Vậy SABC=12.AK.BC≈12.6,783.12=40,696 (cm2)


Gọi H là trung điểm của AC. \(\Delta\)DAC cân tại D.
Do đó DH\(\perp\)AC và AH = \(\frac{1}{2}\)AC (1)
Vẽ AK \(\perp\)BC. Vì \(\Delta\)AKC vuông tại K và ^BCA = 300
nên AK = \(\frac{1}{2}\)AC (2)
Từ (1) và (2) suy ra AK = AH
Xét \(\Delta\)AKB và \(\Delta\)AHD có:
^AKB = ^AHD (=900)
AK = AH(gt)
^BAK = ^DAH (=500)
Do đó \(\Delta\)AKB = \(\Delta\)AHD (g.c.g)
=> AB = AD
Vậy \(\Delta\)ABD cân tại A(đpcm)

Kẻ đường cao AH ứng với BC
Trong tam giác vuông ACH:
\(sinC=\dfrac{AH}{AC}\Rightarrow AH=AC.sinC\)
\(cosC=\dfrac{CH}{AC}\Rightarrow CH=AC.cosC\)
Trong tam giác vuông ABH:
\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=\dfrac{AC.sinC}{tanB}\)
Do đó:
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AH\left(BH+CH\right)=\dfrac{1}{2}.4,5.sin55^0.\left(\dfrac{4,5.sin55^0}{tan60^0}+4,5.cos55^0\right)\approx8,68\left(cm^2\right)\)

(K đăng hình đc nên hình tự vẽ)
Kẻ \(AH\perp BC\left(H\in BC\right)\)
• Xét \(\Delta HAC\) vuông tại \(H\) có
\(\sin C=\dfrac{AH}{AC}\Rightarrow AH=\sin50^o.35\approx26,81\left(cm\right)\)
\(\cos C=\dfrac{HC}{AC}\Rightarrow HC=\cos50^o.35\approx22,5\left(cm\right)\)
• Xét \(\Delta HAB\) vuông tại \(H\) có
\(\tan B=\dfrac{AH}{BH}\Rightarrow BH\approx\dfrac{26,81}{\tan60^o}\approx15,48\left(cm\right)\)
\(\cos B=\dfrac{AH}{AB}\Rightarrow AB\approx\dfrac{26,81}{\cos60^o}\approx53,62\left(cm\right)\)
*Khi đó chu vi \(\Delta ABC\) bằng \(AB+BC+AC\)
\(\approx53,62+\left(22,5+15,48\right)+35\)
\(\approx192,48\left(cm\right)\)
*Khi đó \(S_{\Delta ABC}=\dfrac{AH.BC}{2}\approx\dfrac{26,81.\left(22,5+15,48\right)}{2}\approx509,12\left(cm^2\right)\)
#F.C

A B C H K
Từ A kẻ đường cao AH vuông góc với BC , từ B kẻ đường cao BK vuông góc với AC
=> AH = sinC x AC = sin 500 x 35 = a
Ta có : AB = \(\frac{AH}{sinB}=\frac{a}{sinB}=b\)
BK = \(sinA\times AB=sin\left(180^o-60^o-50^o\right)=sin70^o\times b\)= c
=> S . ABC = 1/2AC x BK = 1/2 x 35 x c =..........
a,b,c mình đặt thay cho độ dài AH , AB, BK
Sao bạn không tính hẳn AH, AB, BK mà phải kí hiệu a, b,c vậy?
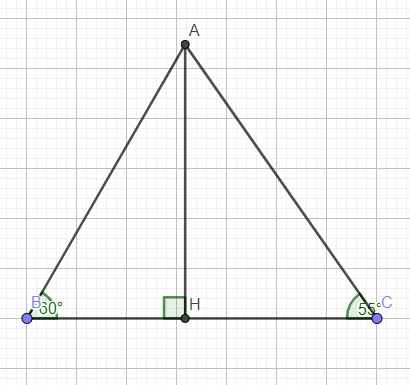
Lời giải:
Dễ tính $\widehat{A}=180^0-(\widehat{B}+\widehat{C})=70^0$
Theo công thức sin:
\(\frac{AB}{\sin A}=\frac{BC}{\sin B}=\frac{AC}{\sin C}\)
\(\Leftrightarrow \frac{AB}{\sin 70}=\frac{BC}{\sin 60}=\frac{35}{\sin 50}\)
\(\Rightarrow AB=\sin 70.\frac{35}{\sin 50}\approx 43\) (cm); \(BC=\sin 60.\frac{35}{\sin 50}\approx 40\) (cm)
Chu vi tam giác $ABC$ là:
$AB+BC+AC=43+40+35=118$ (cm)
Diện tích tam giác $ABC$ là: $\frac{1}{2}AB.AC\sin A=\frac{1}{2}.43.35.\sin 70\approx 707$ (cm vuông)