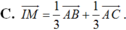NK
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 6 2018
1,Ta có luôn tồn tại một điểm K sao cho \(4\overrightarrow{AB}-\overrightarrow{AC}=3\overrightarrow{AK}\).(*) Thật vậy:
VT(*) = \(4\left(\overrightarrow{AK}+\overrightarrow{KB}\right)-\left(\overrightarrow{AK}+\overrightarrow{KC}\right)=3\overrightarrow{AK}+4\overrightarrow{KB}-\overrightarrow{KC}\) (**)
Từ (*) và (**) ta có : \(4\overrightarrow{KB}-\overrightarrow{KC}=\overrightarrow{0}\) ⇔\(4\overrightarrow{KB}=\overrightarrow{KC}\) ⇒ B nằm giữa K và C sao cho 4KB = KC= \(\dfrac{4}{3}\) .BC.
Khi đó ta có : \(\left|4\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{3AK}\right|=3AK\)
Ap dụng định lí Py-ta-go cho tam giác ABC vuông tại A ta được:
BC2= AB2 + AC2 ⇒BC = \(\sqrt{2^2+2^2}=2\sqrt{2}\)⇒ KC = \(\dfrac{4}{3}\).BC = \(\dfrac{4}{3}\). \(2\sqrt{2}\)
⇒KC = \(\dfrac{8\sqrt{2}}{3}\)
Ta có : tam giác ABC vuông cân tại A nên \(\widehat{ACB}=\widehat{ACK}=45^O\)
Ap dụng định lí cosin ta có : Trong tam giác ACK có
AK = \(\sqrt{AC^2+KC^2-2AK.KC.\cos\widehat{ACK}}=\sqrt{2^2+\left(\dfrac{8\sqrt{2}}{3}\right)^2-2.2.\dfrac{8\sqrt{2}}{3}.\cos45^O}=\dfrac{2\sqrt{17}}{3}\)
⇒3AK=2\(\sqrt{17}\)⇒ \(\left|4\overrightarrow{AB}-\overrightarrow{AC}\right|\)=2\(\sqrt{17}\)
VẬY.....................
MN
21 tháng 8 2019
Câu 2: AM=3MB => vt AC + vt CM = 3vtMC + 3vtCB
<=>vtCM - 3vtMC = 3vtCB -vtAC
<=>vtCM = 1/4 vtCA + 3/4 vtCB
(Mk mới học Toán 10 nên có sai thì thông cảm nha!!!)
HT
28 tháng 7 2019
a/ Có AM= 3MB\(\Rightarrow\overrightarrow{AM}=3\overrightarrow{MB}\)
Theo quy tắc 3 điểm=> \(\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{AM}\)
và \(\overrightarrow{CM}=\overrightarrow{CB}-\overrightarrow{MB}\)
Cộng vế vs vế=> \(2\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{AM}+\overrightarrow{CB}-\overrightarrow{MB}\)
\(\Leftrightarrow2\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{MB}+\overrightarrow{CB}\)
\(\Leftrightarrow2\overrightarrow{CM}=\overrightarrow{CA}+\frac{2}{3}\overrightarrow{AB}+\overrightarrow{CB}\)
\(\Leftrightarrow6\overrightarrow{CM}=3\overrightarrow{CA}+2\overrightarrow{\:AB}+3\overrightarrow{CB}\)
\(\Leftrightarrow6\overrightarrow{CM}=\overrightarrow{CA}+5\overrightarrow{CB}\) ( vì \(2\overrightarrow{CA}+2\overrightarrow{AB}=2\overrightarrow{CB}\) )
b/ Làm tương tự câu a
c/ Theo quy tắc trung điểm có:
\(2\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{CB}\)
\(2\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{AC}\)
\(\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}=2\overrightarrow{AN}+\overrightarrow{BA}+2\overrightarrow{CM}+\overrightarrow{AC}\)
\(=2\overrightarrow{AN}+\overrightarrow{BC}+2\overrightarrow{CM}\)
Có \(\overrightarrow{BC}=2\overrightarrow{BN}=2\left(\overrightarrow{BA}+\overrightarrow{AN}\right)\)
=>\(\overrightarrow{AB}=2\overrightarrow{AN}+2\overrightarrow{BA}+2\overrightarrow{AN}+2\overrightarrow{CM}\)
\(\Leftrightarrow3\overrightarrow{AB}=4\overrightarrow{AN}+2\overrightarrow{CM}\Leftrightarrow\overrightarrow{AB}=\frac{4}{3}\overrightarrow{AN}+\frac{2}{3}\overrightarrow{CM}\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2020
Đặt \(\left\{{}\begin{matrix}\frac{1}{x+3y-1}=X\\\frac{1}{2x-y+3}=Y\end{matrix}\right.\)
Hệ phương trình trở thành:
\(\left\{{}\begin{matrix}2X-Y=5\\X+2Y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4X-2Y=10\\X+2Y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5X=15\\X+2Y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}X=3\\Y=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{1}{x+3y-1}=3\\\frac{1}{2x-y+3}=1\end{matrix}\right.\) (nhân chéo) \(\Leftrightarrow\left\{{}\begin{matrix}x+3y-1=\frac{1}{3}\\2x-y+3=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+3y=\frac{4}{3}\\2x-y=-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+3y=\frac{4}{3}\\6x-3y=-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+3y=\frac{4}{3}\\7x=-\frac{14}{3}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-\frac{2}{3}\\y=\frac{2}{3}\end{matrix}\right.\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(-\frac{2}{3};\frac{2}{3}\right)\)
CM
14 tháng 8 2017
Chọn C.
Theo định lí hàm cosin, ta có : 
Do MC = 2MB nên BM = 1/3.BC = 2.
Theo định lí hàm cosin, ta có: AM2 = AB2 + BM2 - 2AB.BM.cos B = 42 + 22 -2.4.2.1/2 = 12
Do đó: 
.
