Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

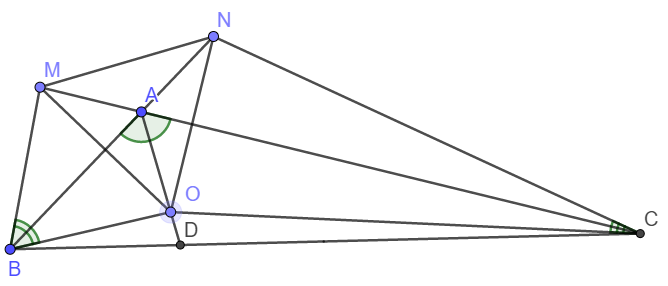
a) Xét tam giác ABC có \(\widehat{B}+\widehat{C}=60^o\Rightarrow BAC=120^o\)
Do AD là phân giác nên \(\widehat{BAD}=\widehat{CAD}=60^o\)
\(\widehat{MAB}\) và \(\widehat{BAC}\) là hai góc kề bù nên \(\widehat{MAB}=180^o-120^o=60^o\)
Vậy thì \(\Delta MAB=\Delta OAB\left(g-c-g\right)\)
\(\Rightarrow AM=AO\)
Hoàn toàn tương tự ta có AN = AO
Vậy nên AM = AN.
b) Ta có do \(\Delta MAB=\Delta OAB\Rightarrow AM=AO;BM=BO\)
Suy ra AB là trung trực của MO,.
Lại có N thuộc AB nên NM = NO
Hoàn toàn tương tự ta có MO = MN
Vậy OM = ON = MN hay OMN là tam giác đều.

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Hoàng Giang - Toán lớp 7 - Học toán với OnlineMath


a) Xét tam giác ABC có ˆB+ˆC=60o⇒BAC=120oB^+C^=60o⇒BAC=120o
Do AD là phân giác nên ˆBAD=ˆCAD=60oBAD^=CAD^=60o
ˆMABMAB^ và ˆBACBAC^ là hai góc kề bù nên ˆMAB=180o−120o=60oMAB^=180o−120o=60o
Vậy thì ΔMAB=ΔOAB(g−c−g)ΔMAB=ΔOAB(g−c−g)
⇒AM=AO⇒AM=AO
Hoàn toàn tương tự ta có AN = AO
Vậy nên AM = AN.
b) Ta có do ΔMAB=ΔOAB⇒AM=AO;BM=BOΔMAB=ΔOAB⇒AM=AO;BM=BO
Suy ra AB là trung trực của MO,.
Lại có N thuộc AB nên NM = NO
Hoàn toàn tương tự ta có MO = MN
Vậy OM = ON = MN hay OMN là tam giác đều.
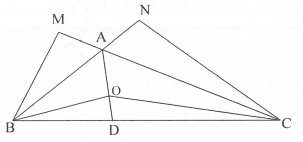 Ta có: △ABC có góc B+góc C=60 độ
Ta có: △ABC có góc B+góc C=60 độ
➩góc BAC =120 độ
ta có AD là phân giác
góc BAC=>BAD=CAD=\(\dfrac{1}{2}\)BAC=60 độ
△ABO và ΔABM có góc BAO= BAM=60 độ
AB chung
góc ABM =ABO
➩tam giác ABO =tam giác ABM (g.c.g)
➝AM=AO (*)
Ta chứng minh tương tự như trên:
tam giác ACO= tam giác ACN (g.c.g)
➝AN=AO(**)
Từ (*)(**) ⇒AM=AN (đpcm)

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Hoàng Giang - Toán lớp 7 - Học toán với OnlineMath

Ta có hình vẽ sau:
D E B M C 1 2 1 2 A
a) Vì AB = AC => ΔABC cân
=> \(\widehat{B_2}=\widehat{C_1}\)
Xét ΔABM và ΔACM có:
AB = AC (gt)
\(\widehat{B_2}=\widehat{C_1}\left(cmt\right)\)
BM = CM (gt)
=> ΔABM = ΔACM(c.g.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 góc tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^o\) (kề bù)
=> \(\widehat{AMB}=\widehat{AMC}=\frac{180^o}{2}=90^o\)
=> AM \(\perp\) BC(đpcm)
b) Ta có: \(\widehat{B_2}=\widehat{C_1}\) và \(\widehat{B_1}+\widehat{B_2}=180^o;\widehat{C_1}+\widehat{C_2}=180^o\)
=> \(\widehat{B_1}=\widehat{C_2}\)
Xét ΔABD và ΔACE có:
AB = AC(gt)
\(\widehat{B_1}=\widehat{C_2}\left(cmt\right)\)
BD = CE (gt)
=> ΔABD = ΔACE(c.g.c)
=> \(\widehat{BAD}=\widehat{CAE}\) (2 góc tương ứng)
mà \(\widehat{BAM}=\widehat{CAM}\) (ΔABM = ΔACM)
=> \(\widehat{BAD}+\widehat{BAM}=\widehat{CAE}+\widehat{CAM}\)
=> AM là tia p/g của \(\widehat{DAE}\) (đpcm)

a: Ta có: \(\widehat{ABC}+\widehat{ABM}=180^0\)(hai góckề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
=>AM=AN
=>ΔAMN cân tại A
b: Xét ΔBME vuông tại E và ΔCNF vuông tại F có
BM=CN
\(\widehat{BME}=\widehat{CNF}\)(ΔABM=ΔACN)
Do đó: ΔBME=ΔCNF
c: Ta có: ΔBME=ΔCNF
=>ME=NF
Ta có: AE+EM=AM
AF+FN=AN
mà AM=AN và ME=NF
nên AE=AF
Xét ΔAEO vuông tại E và ΔAFO vuông tại F có
AO chung
AE=AF
Do đó: ΔAEO=ΔAFO
=>\(\widehat{EAO}=\widehat{FAO}\)
=>\(\widehat{MAO}=\widehat{NAO}\)
=>AO là phân giác của góc MAN
d: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
AM=AN
Do đó: ΔAMH=ΔANH
=>\(\widehat{MAH}=\widehat{NAH}\)
=>AH là phân giác của góc MAN
mà AO là phân giác của góc MAN
nên A,O,H thẳng hàng