Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

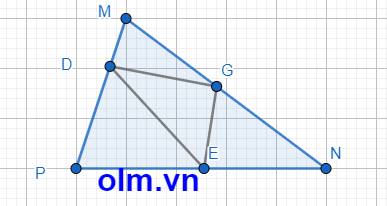
Tỉ số diện tích tam giác PDE và diện tích tứ giác DMNE là:
1 : 2 = \(\dfrac{1}{2}\)
Ta có sơ đồ: 
Theo sơ đồ ta có: Diện tích tam giác BDE = 360 : (1+2) = 120 (cm2)
Diện tích tứ giác DMNE là: 360 - 120 = 240 (cm2)
SMEP = \(\dfrac{1}{2}\)SMNP vì ( hai tam giác có chung đường cao hạ từ đỉnh M xuống đáy PN và PE = \(\dfrac{1}{2}\) PN)
SMEP = 360 \(\times\) \(\dfrac{1}{2}\) = 180(cm2)
Tỉ số diện tích SDEP và SMEP là: 120 : 180 = \(\dfrac{2}{3}\) ⇒ PD = \(\dfrac{2}{3}\) PM ( vì hai tam giác có chung đường cao hạ từ đỉnh E xuống đáy PM nên tỉ số diện tích hai tam giác là tỉ số của hai cạnh đáy)
Cạnh MD bằng: 1 - \(\dfrac{2}{3}\) = \(\dfrac{1}{3}\) (cạnh PM)
SMGD = \(\dfrac{1}{3}\) SMGP ( Vì hai tam giác có chung đường cao hạ từ đỉnh G xuống đáy PM và MD = \(\dfrac{1}{3}\) PM)
SMGP = \(\dfrac{1}{2}\) SMNP ( Vì hai tam giác có chung đường cao hạ từ đỉnh P xuống đáy MN và MG = \(\dfrac{1}{2}\) MN)
⇒ SMGP = \(\dfrac{1}{3}\) \(\times\) \(\dfrac{1}{2}\) SMNP = \(\dfrac{1}{3}\) \(\times\) \(\dfrac{1}{2}\) \(\times\) 360 = 60 (cm2)
SGEN = \(\dfrac{1}{2}\)SGPN ( vì hai tam giác có chung đường cao hạ từ đỉnh G xuông đáy PN và EN = \(\dfrac{1}{2}\)PN)
Tương tự ta có: SGPN = \(\dfrac{1}{2}\) SMNP
⇒ SGEN = \(\dfrac{1}{2}\) \(\times\) \(\dfrac{1}{2}\) \(\times\) 360 = 90 (cm2)
SGDE = SMNED - SMGD - SGEN = 240 - 60 -90 = 90 (cm2)
Đáp số: 90 cm2