Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A B C
a, Xét tam giác ABC vuông tại A, áp dụng định lí Pytago ta có:
BC2 = AB2 + AC2
BC2 = 212 + 722
BC2 = 5625
BC = 75 (cm)
b, Tam giác ABC vuông tại A, đường cao AH
Ta có: AB2 = BH . BC (định lí 1)
212 = BH . 75
BH = 441 : 75
BH = 5,88 (cm)
Ta có : BC = BH + HC
75 = 5,88 + HC
HC = 75 - 5,88
HC = 69,12 (cm)
Ta có: AH2 = BH . HC
AH2 = 5,88 . 69,12
AH2 = 406,4256
AH = 20,16 (cm)
c, (Bạn tự vẽ tia p/g nha)
Theo tính chất đường phân giác góc B ta có:
=> AD/ DC = AB/ BC
=> AD/ AB = DC/BC
=> AD/ 21 = DC/ 75
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
AD/21 = DC/ 75 = AD + DC/ 21 + 75 = AC/ 96 = 72/ 96 = 3/4
=> AD/ 21 = 3/4 => AD = 15,75 (cm)
=> DC/ 75 = 3/4 => DC = 56, 25 (cm)
Mình không biết bạn có đánh sai số hay không mà số chênh nhau lớn quá, nếu bạn đánh sai thì chỉ cần thay số trong bài mình làm cho bạn là được nha :33
CHÚC BẠN HỌC TỐT !!!
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}=53^0\)
=>\(\widehat{C}=37^0\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=4,8(cm)
a. Ta có: AB2 = 62 = 36
AC2 = 4,52 = 20,25
BC2 = 7,52 = 56,25
Vì AB2 + AC2 = 36 + 20,25 = 56,25 = BC2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
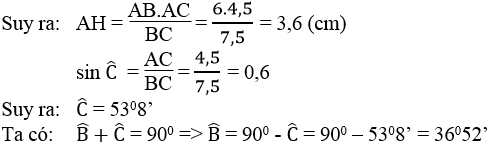b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
Ta có \(\Delta CAB\sim\Delta CDB\left(g.g\right)\Rightarrow\dfrac{CB}{CD}=\dfrac{CA}{CB}\)
\(\Rightarrow CB^2=CD\cdot CA\)
Ta có \(CA=CD+DA=16\left(cm\right)\)
\(\Rightarrow CB^2=9\cdot16=144\Rightarrow CB=12\left(cm\right)\)
Ta có \(\dfrac{DB}{BA}=\dfrac{CB}{CA}=\dfrac{12}{16}=\dfrac{3}{4}\)
\(\Rightarrow DB=\dfrac{3}{4}AB=18\left(cm\right)\)