Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để chứng minh QO⋅QMOP⋅PM=HF^2/HE^2, ta sẽ sử dụng định lí hình học và tính chất của các tam giác đồng dạng.
Đầu tiên, ta cần chứng minh tam giác QOM và tam giác MOP đồng dạng. Ta có:
∠QOM = ∠MOP (do chúng là góc đối) ∠OQM = ∠OMP (do chúng là góc ở chung) => Tam giác QOM đồng dạng với tam giác MOP theo định lí góc-góc (AA).
Từ đó, ta có tỷ lệ giữa các cạnh của hai tam giác này:
QM/OP = OQ/OM (tỷ lệ cạnh tương ứng của hai tam giác đồng dạng) => QM = OQ/OM * OP
Tiếp theo, ta cần chứng minh tam giác HEF và tam giác HOM đồng dạng. Ta có:
∠HEF = ∠HOM (do chúng là góc đối) ∠EHF = ∠OHM (do chúng là góc ở chung) => Tam giác HEF đồng dạng với tam giác HOM theo định lí góc-góc (AA).
Từ đó, ta có tỷ lệ giữa các cạnh của hai tam giác này:
HE/OM = EF/OM (tỷ lệ cạnh tương ứng của hai tam giác đồng dạng) => HE = EF/OM * OM => HE = EF
Như vậy, ta có HE = EF.
Bây giờ, ta sẽ xem xét tỷ lệ giữa các đoạn thẳng QO, QM, OP, PM và HF, HE:
QO⋅QMOP⋅PM = (OQ/OM * OP) * (OP) * (PM) = OQ * OP * PM / OM = OQ * PM
Vì HE = EF, nên ta có:
HF/HE = QM/OM (tỷ lệ cạnh tương ứng của hai tam giác đồng dạng HEF và HOM) => HF = QM/OM * HE
Thay giá trị của HE = EF vào, ta có:
HF = QM/OM * EF
Vậy, ta thấy HF^2 = (QM/OM * EF)^2
Như vậy, ta có:
QO⋅QMOP⋅PM = HF^2/HE^2
Vậy, điều phải chứng minh đã được chứng minh.

a: Xét ΔOAM vuông tại A có cosAOM=OA/OM=1/2
nên góc AOM=60 độ
=>góc AOB=60 độ
=>sđ cung AB=60 độ
b: Xét (O) có
MA,MC là tiếp tuyến
nên MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc với AC
c: Xét ΔOAB có OA=OB và góc AOB=60 độ
nên ΔOAB đều
mà AH là đườg cao
nên H là trung điểm của OB
=>HO=HB
Vì MO là trung trực của AC
nên MO vuông góc AC tại H và H là trung điểm của AC
HA*HC=HA^2
HO*HM=HA^2
=>HA*HC=HO*HM
=>HA*HC=HB*HM
d: Xét ΔOBC có OB=OC và góc BOC=60 độ
nên ΔBCO đều
=>OB=OC=BC=OA=AB
=>OA=AB=BC=OC
=>OABC là hình thoi

Vì \(AM\perp AH\left(gt\right)\)(1)
và \(BC\perp AH\left(gt\right)\)(2)
Từ(1) và (2)
\(\Rightarrow AM//BC\)(T/c )
Mà \(EF//BC\)(* )
Do \(\widehat{AEF}=\widehat{ABC}\)(do vị trí đồng vị )'
\(\Rightarrow AH\perp EF\)(*)
Mà \(AM\perp AH\left(gt\right)\)(** )
Từ (*) và (** )
\(\Rightarrow AM\perp EF\)
( đpcm)

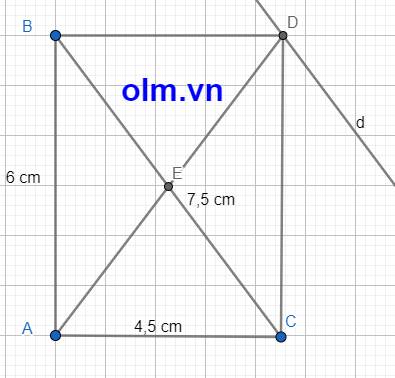
a, Xét \(\Delta\)ABC có: AB2 + AC2 = 62 + 4,52 = 56,25 (cm2)
BC2 = 7,52 = 56,25 (cm2)
AB2 + AC2 = BC2 vậy tam giác ABC vuông tại A (đpcm)
SinC = 6 : 7,5 =0,8 ⇒ \(\widehat{C}\) = 53,130 ⇒ \(\widehat{B}\) = 900 - 53,130 = 36,870
b, Dựng hình chữ nhật ABCD, chiều cao AH, DK, và đường thẳng d đi qua D song song với BC như hình vẽ ta có
SABC = SBDC ⇒ AH = DK
Lây 1 điểm bất M kỳ di động trên đường thẳng d ta có:
SBDC = SMBC (vì hai tam giác có chiều cao bằng nhau và chung cạnh đáy BC)
⇒ SABC = SMBC
Kết luận khi M di động trên đường thẳng d thì diện tích tam giác MBC luôn bằng diện tích tam giác ABC