K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

QD
20 tháng 4 2017
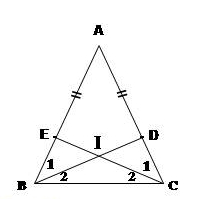
∆ABD và ∆ACE có:
AB=AC(gt)
ˆA góc chung.
AD=AE(gt)
Nên ∆ABD=∆ACE(c.g.c)
Suy ra: ˆABD=ˆACE.
Tức là ˆB1 =ˆC1
b) Ta có ˆB=ˆC mà ˆB1=ˆC1 suy ra ˆB2=ˆC2
Vậy ∆IBC cân tại I
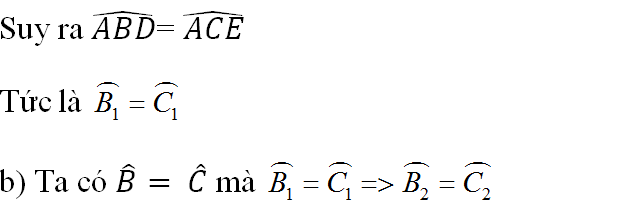
a/
AD=AE (gt)
AB=AC (gt)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\) => DE//BC (Talet đảo trong tg)
=> BDEC là hình thang
Ta có
tg ABC cân tại A \(\Rightarrow\widehat{B}=\widehat{C}\) (góc ở đáy tg cân)
=> BDEC là hình thang cân
b/
Xét tg ABC
\(\widehat{B}+\widehat{C}=2\widehat{B}=180^o-\widehat{A}=180^o-50^o=130^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=\dfrac{130^o}{2}=65^o\)
...