Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

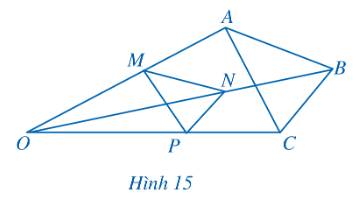
Xét tam giác OAB có \(\frac{{OM}}{{MA}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Xét tam giác OBC có \(\frac{{OP}}{{PC}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Từ đó ta có \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}}\).
Xét tam giác OAC với \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}} \Rightarrow MP\parallel AC\) (Hệ quả của định lý Thales).

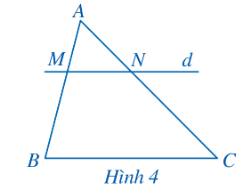
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra:MN//BC
hay BMNC là hình thang

Xét tam giác ABC với \(MN\parallel BC\), ta có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) (định lý Thales).

1.
AB=CD (cặp cạnh đối hbh)
AM=AB/2 và CN=CD/2
=> AM=CN (1)
AM thuộc AB; CN thuộc CD mà AB//CD => AM//CN (2)
Từ (1) và (2) => AMCN là hbh(Tứ giác có một cặp cạnh đối // và = nhau thì tứ giác đó là hbh)
2.
a. M là trung điểm AB; N là trung điểm AC => MN là đường trung bình của tgABC
=> MN//BC => MN//BP và MN=BP=BC/2
=> BMNP là hbh (lý do như bài 1)
b. Ta có BMNP là hbh và ^B=90 => BMNP là HCN
\(BC=\sqrt{AC^2-AB^2}=\sqrt{5^2-3^2}=4cm.\)
Từ kq câu a => MN=BC/2=4/2=2 cm
C/m tương tự câu a có NP là đường trung bình của tg ABC => NP=AB/2=3/2=1,5 cm
Chu vi BMNP là
(2+1,5)x2=7 cm

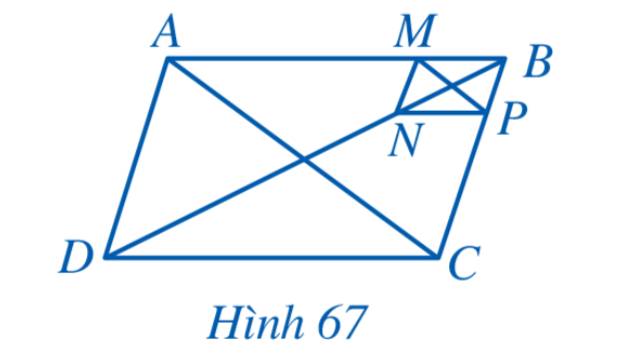
a) Vì ABCD và BMNP là hình bình hành nên \(MN//BP\) và \(AD//BC \Rightarrow MN//AD\)
Xét tam giác ABD có \(AD//MN \Rightarrow \frac{{BM}}{{BA}} = \frac{{BN}}{{BD}}\) (1) (Định lý Thales)
Tương tự ta chứng minh được \(NP//DC \Rightarrow \frac{{BN}}{{BD}} = \frac{{BP}}{{BC}}\)(2)
Từ (1) và (2) ta có \(\frac{{BM}}{{BA}} = \frac{{BP}}{{BC}}\).
b) Ta có \(\frac{{BM}}{{BA}} = \frac{{BP}}{{BC}} \Rightarrow MP//AC\)(Định lý Thales đảo)
\( \Rightarrow \Delta PBM \backsim\Delta CBA\) (c-c-c) (3)
Vì BMNP là hình bình hành nên ta có \(\frac{{PB}}{{MN}} = \frac{{BM}}{{NP}} = \frac{{MP}}{{PM}} = 1\)
\( \Rightarrow \Delta PBM \backsim\Delta MNP\) (c-c-c) (4)
Từ (3) và (4) ta có \(\Delta MNP \backsim\Delta CBA\).

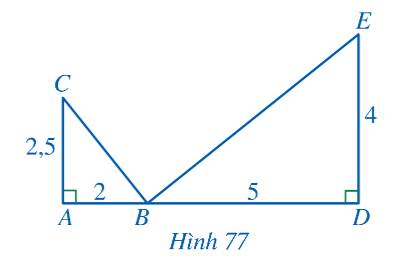
a) Ta thấy \(\frac{{AB}}{{DE}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{AC}}{{DB}} = \frac{2,5}{5} = \frac{1}{2}\)
\( \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\)
Xét tam giác ABC và tam giác DEB có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\) và \(\widehat {CAB} = \widehat {BDE} = 90^\circ \)
\( \Rightarrow \Delta ABC \backsim \Delta DEB\) (c-g-c)
\( \Rightarrow \widehat {ABC} = \widehat {BED}\)
b) Vì \(\Delta ABC \backsim \Delta DEB\) nên \(\widehat {ACB} = \widehat {DBE}\)
Mà tam giác ABC vuông tại A nên \(\widehat {ACB} + \widehat {ABC} = 90^\circ \) hay \(\widehat {DBE} + \widehat {ABC} = 90^\circ \)
Ta thấy
\(\begin{array}{l}\widehat {DBE} + \widehat {CBE} + \widehat {ABC} = 180^\circ \\ \Rightarrow \widehat {CBE} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {CBE} = 90^\circ \end{array}\)
Vậy \(BC \bot BE\).

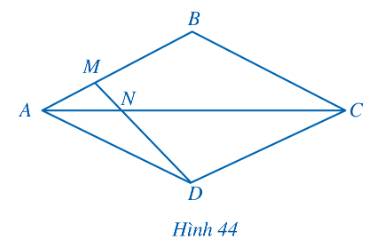
Gọi giao điểm hai đường chéo của hình thoi là O.
Khi đó AC vuông góc với BD tại O.
Vì ABCD là hình thoi nên \(AB = AD\) hay tam giác ABD cân tại A.
Khi đó AO vừa là đường cao, vừa là phân giác của tam giác ABD.
Xét tam giác AMD với AN là đường phân giác, ta có:
\(\frac{{ND}}{{NM}} = \frac{{AD}}{{AM}}\,\,\left( 1 \right)\) (Tính chất đường phân giác)
Mà \(AB = 3AM \Rightarrow \frac{{AB}}{{AM}} = 3 \Rightarrow \frac{{AD}}{{AM}} = 3\,\,\left( 2 \right)\)
Từ (1) và (2) ta có: \(\frac{{ND}}{{NM}} = 3 \Rightarrow ND = 3NM\).

\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{2}{4} = \frac{1}{2}\\\frac{{A'C'}}{{AC}} = \frac{3}{6} = \frac{1}{2}\\\frac{{B'C'}}{{BC}} = \frac{4}{8} = \frac{1}{2}\end{array}\)
Ta thấy \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
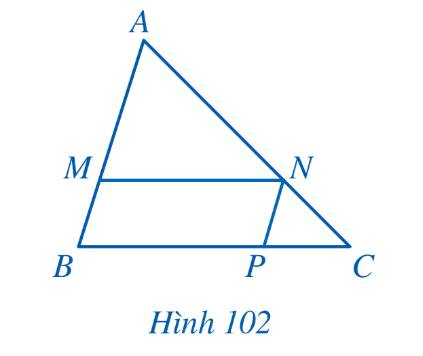

Vì BMNP là hình bình hành nên \(NP\parallel AB\)\(,\,\,MN = BP,\,\,BM = PN\)
\( \Rightarrow \frac{{NP}}{{AB}} = \frac{{CP}}{{CB}}\) (Định lý Thales)
Ta có: \(\frac{{MN}}{{BC}} = \frac{{BP}}{{BC}}\)
Khi đó: \(\frac{{MN}}{{BC}} + \frac{{NP}}{{AB}} = \frac{{BP}}{{BC}} + \frac{{CP}}{{BC}} = \frac{{BC}}{{BC}} = 1\) (đpcm)