Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{18^2+20^2-14^2}{2.18.20}=\dfrac{11}{15}\).
Vậy \(\widehat{A}=42^o50'\).
\(cosB=\dfrac{a^2+c^2-b^2}{2ac}=\dfrac{14^2+20^2-18^2}{2.14.20}=\dfrac{17}{20}\).
Vậy \(\widehat{B}=60^o56'\).
Vậy \(\widehat{C}=180^o-\widehat{A}-\widehat{B}=77^o46'\).

a) \(c^2=a^2+b^2-2abcosC\)
\(=7^2+10^2-2\times7\times10\times cos56^o29\)
\(\approx71,69\Rightarrow c\approx8,5\)
b) \(b^2=a^2+c^2-2accosB\)
\(=2^2+3^2-2\times2\times3\times cos123^o17\)
\(\approx17,4\Rightarrow b\approx4,2\)
c) \(a^2=b^2+c^2-2bccosA\)
= \(0^2+12^2-2\times0\times12\times cos23^o28\)
\(=144\Rightarrow a\approx12\)

Áp dụng định lý cô sin trong tam giác ABC:
\(c^2=a^2+b^2-2abcosC=7^2+23^2-2.7.23.cos130\)\(\cong784cm\).
Vậy \(c=28cm.\)
\(cosA=\dfrac{c^2+b^2-a^2}{2bc}=\dfrac{28^2+23^2-7^2}{2.23.28}=\dfrac{158}{161}\).
\(\Rightarrow\widehat{A}\cong11^o\).
\(\widehat{B}=180^o-\left(\widehat{A}+\widehat{C}\right)=180^o-\left(130^o+11^o\right)=39^o\).

\(\widehat{B}=180^o-\left(40^o+120^o\right)=20^o\).
A C B 35 H
\(AH=AB.sinB=35.sin20^o\cong12cm.\)
\(\widehat{HCA}=180^o-120^o=60^o\).
\(AH=AC.sin60^o\Rightarrow AC=\dfrac{AH}{sin60}=\dfrac{12}{\dfrac{\sqrt{3}}{2}}=8\sqrt{3}\).
Áp dụng định lý Cô-sin:
\(BC=\sqrt{AB^2+AC^2-2.AB.AC.sinA}\)\(=\sqrt{35^2+\left(8\sqrt{3}\right)^2-2.35.8\sqrt{3}.cos40^o}\cong26cm\).
Vậy \(a=26cm;b=8\sqrt{3}cm,\)\(\widehat{B}=20^o\).
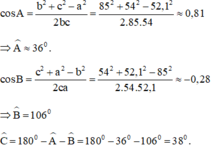



Từ định lí cosin a2 = b2 + c2 - 2bc. cosA
ta suy ra cos A =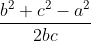 =
= 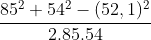
=> cosA ≈ 0,8089 =>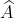 = 360
= 360
Tương tự, ta tính được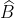 ≈ 1060 28’ ;
≈ 1060 28’ ; 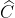 ≈ 370 32’.
≈ 370 32’.