Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

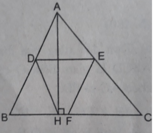
S D E C H = 22 c m 2 ; S B D E F = 20 c m 2 ; S D E F H = 12 c m 2

a. xét tam giác ABC và tam giác HAC có
góc ACB= góc HCA ( góc chung)
góc BAC = góc AHC (=90độ)
do đó tam giác ABC đồng dạng với tam giác HAC(g.g)
b. theo bài ra ta có góc BAC=90 độ
suy ra tam giác ABC vuôg tại A
ta lại có AB=6cm, AC=8cm
suy ra AB ^2+ AC^2= BC^2
thay vào ta có 6^2+ 8^2= BC^2
suy ra BC^2= 10^2
suy ra BC = 10 (cm)

\(\Delta ABC\)cân tại A có AH là đường cao \(\Rightarrow\)H là trung điểm BC \(\Rightarrow HB=HC=\frac{BC}{2}=5\left(cm\right)\)
Xét \(\Delta ABH\)vuông tại H ta có: \(AH^2+BH^2=AB^2\)( định lý Pytago )
\(\Rightarrow AH^2+5^2=13^2\)\(\Rightarrow AH^2=144\)\(\Rightarrow AH=12\left(cm\right)\)
mà O là trung điểm AH \(\Rightarrow OA=OH=\frac{AH}{2}=6\left(cm\right)\)
Xét \(\Delta AOG\)và \(\Delta ABH\)có: +) Chung chiều cao hạ từ B xuống AH
+) \(OA=\frac{1}{2}AH\)
\(\Rightarrow S_{AOG}=\frac{1}{2}S_{ABH}\)
Tương tự ta có: \(S_{AOP}=\frac{1}{2}S_{AHC}\)
\(\Rightarrow S_{AOG}+S_{AOP}=\frac{1}{2}\left(S_{ABH}+S_{AHC}\right)\)
\(\Rightarrow S_{AGOP}=\frac{1}{2}S_{ABC}=\frac{1}{2}.\frac{1}{2}AH.BC=\frac{1}{4}.12.10=30\left(cm^2\right)\)
Vậy \(S_{AGOP}=30\left(cm^2\right)\)

Đáp án:

a) Theo Pytago ta có:
BC2 = AB2 + AC2 = 62 + 82 = 100
=>BC = \(\sqrt{100}\) = 10 (cm).
b) SABC = \(\frac{1}{2}\) . AB . AC = \(\frac{1}{2}\) . AH . BC
=> AH = \(\frac{AB.AC}{BC}\) = \(\frac{6.8}{10}\) = 4,8 (cm).
c) TA có tứ giác AEHF có 3 góc vuông tại A,E,F
=> AEHF là hình chữ nhật
=> EF= AH = 4,8 cm
d) Do EM và EN là đường trung tuyến của tam giác BEH và FCH vuông tại E và F
=> EM = BH /2 và FN = HC/2
=> EM + FN = (BH+CH)/2 = BC/2=5cm
=> MNFE là hình thang vuông có 2 đáy EM,FN, đường cao EF.
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay \(BC=\sqrt{100}=10cm\)
Vậy: BC=10cm
b) Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔAHB∼ΔCAB(g-g)
⇒\(\frac{AH}{CA}=\frac{AB}{CB}\)(các cặp cạnh tương ứng tỉ lệ)
⇒\(AH=\frac{AB\cdot AC}{BC}=\frac{6\cdot8}{10}=\frac{48}{10}=4,8cm\)
Vậy: AH=4,8cm
c) Xét tứ giác AEHF có
\(\widehat{EAF}=90^0\)(\(\widehat{BAC}=90^0\), E∈AB, F∈AC)
\(\widehat{AEH}=90^0\)(HE⊥AB)
\(\widehat{AFH}=90^0\)(HF⊥AC)
Do đó: AEHF là hình chữ nhật(dấu hiệu nhận biết hình chữ nhật)
⇒AH=EF(hai đường chéo của hình chữ nhật AEHF)
mà AH=4,8cm(cmt)
nên EF=4,8cm
Vậy: EF=4,8cm