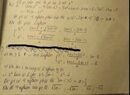Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Đặt \(x^2-2x+m=t\), phương trình trở thành \(t^2-2t+m=x\)
Ta có hệ \(\left\{{}\begin{matrix}x^2-2x+m=t\\t^2-2t+m=x\end{matrix}\right.\)
\(\Rightarrow\left(x-t\right)\left(x+t-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=t\\x=1-t\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=x^2-2x+m\\x=1-x^2+2x-m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-x^2+3x\\m=-x^2+x+1\end{matrix}\right.\)
Phương trình hoành độ giao điểm của \(y=-x^2+x+1\) và \(y=-x^2+3x\):
\(-x^2+x+1=-x^2+3x\)
\(\Leftrightarrow x=\dfrac{1}{2}\Rightarrow y=\dfrac{5}{4}\)
Đồ thị hàm số \(y=-x^2+3x\) và \(y=-x^2+x+1\):
Dựa vào đồ thị, yêu cầu bài toán thỏa mãn khi \(m< \dfrac{5}{4}\)
Mà \(m\in\left[-10;10\right]\Rightarrow m\in[-10;\dfrac{5}{4})\)
Có cách nào lm bài này bằng cách lập bảng biến thiên k ạ

\(\dfrac{x_2}{x_1}=\dfrac{x_3}{x_2}=\dfrac{x_2+x_3}{x_1+x_2}=\dfrac{x_2+x_3}{3}\) (1)
\(\dfrac{x_3}{x_2}=\dfrac{x_4}{x_3}=\dfrac{x_3+x_4}{x_2+x_3}=\dfrac{12}{x_2+x_3}\)
\(\Rightarrow\dfrac{x_2+x_3}{3}=\dfrac{12}{x_2+x_3}\Rightarrow x_2+x_3=\pm6\)
Th1: \(x_2+x_3=6\) thế vào (1):
\(\dfrac{x_2}{x_1}=\dfrac{x_3}{x_2}=\dfrac{x_4}{x_3}=\dfrac{6}{3}=2\) \(\Rightarrow\left\{{}\begin{matrix}x_2=2x_1\\x_4=2x_3\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}x_1+x_2=3\\x_3+x_4=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}3x_1=3\\3x_3=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=1;x_2=2\\x_3=4;x_4=8\end{matrix}\right.\)
\(\Rightarrow m=x_1x_2=2\)
Khỏi cần làm TH2 \(x_2+x_3=-6\) nữa, chọn luôn C

Bước 1: Tìm điều kiện của tham số để phương trình có hai nghiệm phân biệt.
Bước 2: Khi phương trình đã có hai nghiệm phân biệt, ta áp dụng Vi-ét để tìm các giá trị của tham số.
Bước 3. Đối chiếu với điều kiện và kết luận bài toán.
xem tr sách của anh
Bài 1:
PT có 2 nghiệm \(\Leftrightarrow\Delta=\left(m+2\right)^2-4\cdot2\ge0\Leftrightarrow m^2+4m-8\ge0\Leftrightarrow\left[{}\begin{matrix}m\le-2-2\sqrt{3}\\m\ge-2+2\sqrt{3}\end{matrix}\right.\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=m+2\\x_1x_2=2\end{matrix}\right.\)
Ta có \(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=\dfrac{9}{2}\Leftrightarrow2\left(x_1^2+x_2^2\right)=9x_1x_2\)
\(\Leftrightarrow2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=18\\ \Leftrightarrow2\left(m+2\right)^2-8=18\\ \Leftrightarrow2m^2+8m+8-8=18\\ \Leftrightarrow m^2+4m-9=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-2+\sqrt{13}\\m=-2-\sqrt{13}\end{matrix}\right.\left(tm\right)\)

PT có 2 nghiệm \(\Leftrightarrow\Delta'\ge0\)
\(\Leftrightarrow\left(m+1\right)^2-\left(m^2-1\right)\ge0\\ \Leftrightarrow m^2+2m+1-m^2+1\ge0\\ \Leftrightarrow m\ge-1\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2-1\end{matrix}\right.\)
Ta có \(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{1}{6}\Leftrightarrow\dfrac{x_1+x_2}{x_1x_2}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{2\left(m+1\right)}{m^2-1}=\dfrac{1}{6}\Leftrightarrow12m+12=m^2-1\\ \Leftrightarrow m^2-12m-13=0\\ \Leftrightarrow\left[{}\begin{matrix}m=13\left(tm\right)\\m=-1\left(tm\right)\end{matrix}\right.\)

Để pt có 2 nghiệm trái dấu \(\Leftrightarrow3m-2< 0\Leftrightarrow m< \dfrac{2}{3}\)
Nếu \(x_1< 0\) thì \(\dfrac{1}{x_1}-3< 0\) trong khi \(\left|\dfrac{1}{x_2}\right|>0\Rightarrow\) không thỏa mãn
Vậy \(x_1>0;x_2< 0\)
Do đó:
\(\dfrac{1}{x_1}-3=\left|\dfrac{1}{x_2}\right|=-\dfrac{1}{x_2}\)
\(\Leftrightarrow\dfrac{1}{x_1}+\dfrac{1}{x_2}=3\Leftrightarrow x_1+x_2-3x_1x_2=0\)
\(\Leftrightarrow-2\left(m-1\right)-3\left(3m-2\right)=0\)
\(\Leftrightarrow m=...\)

\(\Delta=\left(m+2\right)^2-4m=m^2+4>0\) pt luôn có 2 nghiệm pb
Để \(x_1;x_2\ne0\Leftrightarrow m\ne0\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+2\\x_1x_2=m\end{matrix}\right.\)
\(\dfrac{1}{x_1^2}+\dfrac{1}{x_2^2}>1\Leftrightarrow x_1^2+x_2^2>\left(x_1x_2\right)^2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1x_2\right)^2>0\)
\(\Leftrightarrow\left(m+2\right)^2-2m-m^2>0\)
\(\Leftrightarrow2m+4>0\Rightarrow m>-2\)
Có \(10-\left(-1\right)+1-1=11\) giá trị nguyên của m thỏa mãn (loại \(m=0\))

Để phương trình có hai nghiệm thì \(\Delta\ge0\)\(\Leftrightarrow m^2-4\ge0\) \(\Leftrightarrow\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\).
Theo định lý Vi-et: \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=1\end{matrix}\right.\).
Khi đó: \(A=\dfrac{\left(x_1-x_2\right)^2}{x_1+x_2-1}=\dfrac{\left(x_1+x_2\right)^2-4x_1x_2}{x_1+x_2-1}=\dfrac{\left(-m\right)^2-4.1}{-m-1}\)\(=-\dfrac{m^2-4}{m+1}\)\(=-\dfrac{m\left(m+1\right)-\left(m+1\right)-3}{m+1}\)\(=-m-1-\dfrac{3}{m+1}\).
Để A có giá trị nguyên thì \(m+1\inƯ\left(3\right)\) .
Suy ra \(m+1\in\left\{-1;1;-3;3\right\}\).
m + 1 = -1 thì m = - 2.
m + 1 = 1 thì m = 0. (loại).
m + 1 = -3 thì m = -4.
m + 1 = 3 thì m = 2.