Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo định lí Viet \(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=x_1^4+x_2^4=\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2-2x_1^2x_2^2=727\\y_1y_2=x_1^4x_2^4=1\end{matrix}\right.\)
Phương trình cần tìm có dạng \(ax^2+bx+c=0\left(1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}-\dfrac{b}{a}=727\\\dfrac{c}{a}=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=-727a\\c=a\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow ax^2-727ax+a=0\)
\(\Leftrightarrow x^2-727x+1=0\)

Đáp án: D
Theo định lý Vi-ét ta có
Khi đó, ![]() là nghiệm của phương trình
là nghiệm của phương trình

Coi như các điều kiện có nghiệm đều thỏa mãn
Theo định lý Viet \(\left\{{}\begin{matrix}x_1+x_2=-\frac{b}{a}\\x_1x_2=\frac{c}{a}\end{matrix}\right.\)
Giả sử pt bậc 2 nhận \(\frac{1}{x_1};\frac{1}{x_2}\) là nghiệm có dạng \(x^2-Ax+B=0\)
\(\left\{{}\begin{matrix}\frac{1}{x_1}+\frac{1}{x_2}=A\\\frac{1}{x_1x_2}=B\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A=\frac{x_1+x_2}{x_1x_2}=\frac{-\frac{b}{a}}{\frac{c}{a}}=-\frac{b}{c}\\B=\frac{1}{x_1x_2}=\frac{a}{c}\end{matrix}\right.\)
Vậy pt đó có dạng: \(x^2+\frac{b}{c}x+\frac{a}{c}=0\Leftrightarrow cx^2+bx+a=0\)

Phương trình đã cho có nghiệm khi:
\(\Delta'=\left(m+1\right)^2-2\left(m^2+4m+3\right)=-m^2-6m-5\ge0\)
\(\Leftrightarrow-5\le m\le-1\)
Khi đó \(\left\{{}\begin{matrix}x_1+x_2=-m-1\\x_1.x_2=\frac{m^2+4m+3}{2}\end{matrix}\right.\)
\(A=|\frac{m^2+4m+3}{2}+2\left(m+1\right)|=\frac{1}{2}.|m^2+8m+7|\le\frac{1}{2}.|0|=0\)
\(\Rightarrow MaxA=0\Leftrightarrow m=-1\)
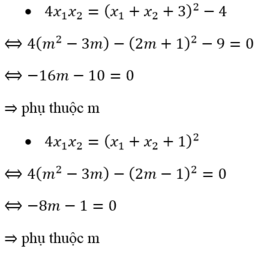
Phương trình có m được chứ?
\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-m^2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y_1+y_2=2\left(x_1+x_2\right)-2=2.2-2=2\\y_1y_2=\left(2x_1-1\right)\left(2x_2-1\right)=-4m^2-3\end{matrix}\right.\)
\(\Rightarrow ptb2:y^2-2y-4m^2-3=0\)