Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

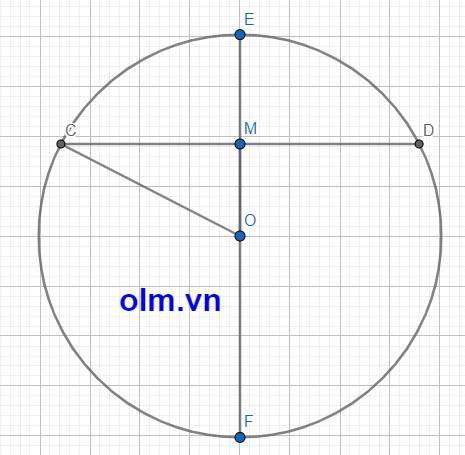
Dây dài nhất đi qua M là đường kính đi qua M của đường tròn.
Dây ngắn nhất đi qua M là dây đi qua M và vuông góc với OM tại M
Dộ dài dây dài nhất đi qua M là: 13 x 2 = 26 (cm)
Độ dài của dây ngắn nhất đi qua M là: CD = CM x 2
CD = 2x \(\sqrt{CO^2-OM^2}\)
CD = 2x\(\sqrt{13^2-5^2}\)
CD = 24 (cm)
Từ những lập luận trên ta có những dây đi qua M có độ dài là số tự nhiên là những dây có độ dài lần lượt là 24cm; 25cm; 26cm
Vậy có 3 dây đi qua M và có độ dài là số tự nhiên.

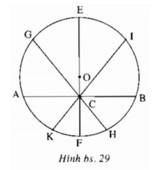
Dây lớn nhất đi qua C là đường kính EF = 50cm. Dây nhỏ nhất đi qua C là dây AB vuông góc với OC tại C, AB = 48 cm.
Có tất cả 4 dây đi qua C có độ dài là một số nguyên xentimet.

a. Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
OA2 = AM2 + OM2
Suy ra: AM2 = OA2 – OM2 = 52 – 32 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (\(\frac{1}{2}\)).AB
Hay: AB = 2AM = 2.4 = 8 (dm)
b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)
a. Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
OA2 = AM2 + OM2
Suy ra: AM2 = OA2 – OM2 = 52 – 32 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (\(\frac{1}{2}\)).AB
Hay: AB = 2AM = 2.4 = 8 (dm)
b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)

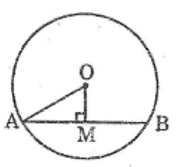
Giả sử AB là một dây cung qua M có độ dài là số tự nhiên. Kẻ dây cung CD qua M và vuông góc với OM. Ta có \(\frac{CD^2}{4}=CM^2=R^2-OM^2=17^2-8^2=9\times16\to CD=24.\)
Kẻ OH vuông góc với AB, ta suy ra \(OH\le OM\to AB\) gần tâm hơn dây CD. Do đó \(24\le AB\le2R=34.\) Do đó \(AB=24,25,\ldots,34.\) Do đó có tối đa \(11\) cung có độ dài như vậy.
Mặt khác với mỗi \(k=24,25,\ldots,34\) ta vẽ đường tròn tâm O bán kính \(r=\sqrt{R^2-\frac{k^2}{4}}=\sqrt{17^2-\frac{k^2}{4}}=\frac{\sqrt{34^2-k^2}}{2}\). Đường tròn này nằm trong đường tròn (O;17). Qua M ta vẽ tiếp tuyến tới đường tròn (O;r) cắt đường tròn (O;R) ở A,B thì AB=k là số tự nhiên
Vậy có cả thảy 11 dây cung như thế.