Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

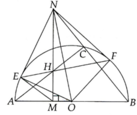
a, Học sinh tự chứng minh
b, N E C ^ = C B E ^ = 1 2 s đ C E ⏜
=> DNEC ~ DNBE (g.g) => ĐPCM
c, DNCH ~ DNMB (g.g)
=> NC.NB = NH.NM = N E 2
DNEH ~ DNME (c.g.c)
=> N E H ^ = E M N ^
d, E M N ^ = E O M ^ (Tứ giác NEMO nội tiếp)
=> N E H ^ = N O E ^ => EH ^ NO
=> DOEF cân tại O có ON là phân giác => E O N ^ = N O F ^
=> DNEO = DNFO vậy N F O ^ = N E O ^ = 90 0 => ĐPCM

(Quá lực!!!)
E N A B C D O H L
Đầu tiên, hãy CM tam giác \(EAH\) và \(ABD\) đồng dạng.
Từ đó suy ra \(\frac{EA}{AB}=\frac{AH}{BD}\) hay \(\frac{EA}{OB}=\frac{AC}{BD}\).
Từ đây CM được tam giác \(EAC\) và \(OBD\) đồng dạng.
Suy ra \(\widehat{ECA}=\widehat{ODB}\). Do đó nếu gọi \(OD\) cắt \(EC\) tại \(L\) thì CM được \(OD⊥EC\).
-----
Đường tròn đường kính \(NC\) cắt \(EC\) tại \(F\) nghĩa là \(NF⊥EC\), hay \(NF\) song song với \(OD\).
Vậy \(NF\) chính là đường trung bình của tam giác \(AOD\), vậy \(NF\) qua trung điểm \(AO\) (là một điểm cố định) (đpcm)