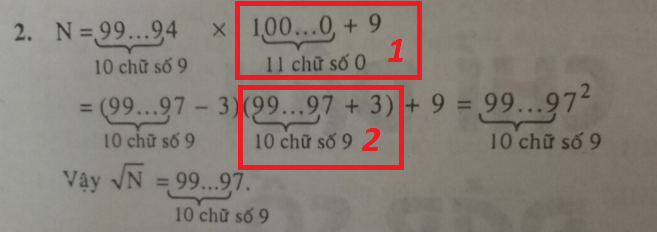Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Tất cả những vấn đề em hỏi đều thuộc lý thuyết phân tích cấu tạo số cơ bản. Tất nhiên, lời giải sẽ có 1 chút tắt (không đáng kể).
Tip: Em chịu khó viết ra nháp từng bước một và đọc kỹ. Nếu thấy số dài mà không hiểu vì sao người ta làm vậy, em thử với bộ số nhỏ hơn có phong cách tương tự (ví dụ 994009)
\(\underbrace{999....9}_{10} 4\underbrace{000..0}_{10}9=\underbrace{999....9}_{10} 4\underbrace{00...0}_{11}+9\)
\(=\underbrace{999....9}_{10}4\times 1\underbrace{00...0}_{11}+9\)
\(=(\underbrace{999....9}_{10}7-3)\times (\underbrace{99....9}_{10}7+3)-9\)
(em tưởng tượng 1000 có 3 chữ số 0 đằng sau, biểu diễn được thành 997+3 có 3-1=2 chữ số 9)

\(S=\left(10-1\right)+\left(100-1\right)+\left(1000-1\right)+...+\left(100..00-1\right)\)
\(S=\left(10^1+10^2+10^3+...+10^n\right)-n\)
Đặt \(P=10^1+10^2+10^3+...+10^n\Rightarrow S=P-n\)
\(10P=10^2+10^3+...+10^{n+1}\)
\(10P-P=9P=\left(10^2+10^3+10^4+...+10^{n+1}\right)-\left(10^1+10^2+...+10^n\right)=10^{n+1}-10=10.\left(10^n-1\right)\)
\(P=\dfrac{10.\left(10^n-1\right)}{9}\Rightarrow S=\dfrac{10.\left(10^n-1\right)}{9}-n\)
Vô tình đi ngang qua :)


N=99......94 x 100...0 +9
(11 số 0)
=(99.....97-3)(99.......97+3)+9
=\(\left(99.....97\right)^2-9+9\)
=\(\left(99....97\right)^2\)
\(\Rightarrow\sqrt{N}=\sqrt{\left(99...97\right)^2}=99...97\)

Câu b ra (15.10^n)-3 nhé, đang xài đt ko gõ công thức được
Câu a hình như là vô hạn dấu căn phải ko? Nếu vô hạn thì em nhớ có một cách làm như sau:
a)Đặt \(a=\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{...}}}}>0\)
Bình phương 2 vế lên suy ra \(a^2=6+a\Rightarrow a^2-a-6=0\Rightarrow\left[{}\begin{matrix}a=3\\a=-2\left(L\right)\end{matrix}\right.\)
Vậy a = 3
Em làm đúng không ạ? @Nguyễn Việt Lâm

Công bố:
Ta cần chứng minh số có dạng \(224999...91000...09\)(n-2 cs 9 nằm giữa 4 và 1; n chữ số 0) đều là các số chính phương.
Thật vậy, ta có \(224999...91000...09=224999...91000...000+9=224999...90000...000+10^{n+1}+9\)
n-2 cs 9 n cs 0 n-2 cs 9 n+1 cs 0 n-2 cs 9 n+2 cs 0
\(=224999...9.10^{n+2}+10^{n+1}+9=\left(224000...00+999...9\right).10^{n+2}+10^{n+1}+9\)
n-2 cs 9 n-2 cs 0 n-2 cs 9
\(=\left(224.10^{n-2}+10^{n-2}-1\right).10^{n+2}+10^{n+1}+9=224.10^{2n}+10^{2n}-10^{n+2}+10^{n+1}+9\)\(=225.10^{2n}-100.10^n+10.10^n+9=\left(15.10^n\right)^2-90.10^n+9\)\(=\left(15.10^n\right)^2-2.15.10^n.3+3^2=\left(15.10^n-3\right)^2\)là số chính phương.
Vậy \(224999...91000...09\)(n-2 cs 9 nằm giữa 4 và 1; n chữ số 0) là số chính phương.
\(\Rightarrowđpcm\)

1. So sánh 23−2√193 và√27
2. Chứng minh rằng với x ≥ 1 thì √x+2√x−1 +√x−2√x−1 = 2 nếu 1≤ x≤ 2 và 2√x−1 nếu x>2
3. Cho N= 99...9 400...09 .Tính √N
1. So sánh 23−2√193 và√27
2. Chứng minh rằng với x ≥ 1 thì √x+2√x−1 +√x−2√x−1 = 2 nếu 1≤ x≤ 2 và 2√x−1 nếu x>2
3. Cho N= 99...9 400...09 .Tính √N
10 chữ số 9 10 chữ số 0
10 chữ số 9 10 chữ số 0