Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) CT : Trong đoạn mạch nối tiếp: \(R_{td}\)=\(R_1\)+\(R_2\)+....
b) Điện trờ tương đương của đoạn mạch:
\(R_{td}\)=\(R_1\)+\(R^{_2}\)=20+30=50(Ω)

a) Điện trở tương đương:
\(R_{tđ}=R_1+R_2\left(\Omega\right)\)
b) Cho biết:
\(R_1=20\Omega\)
\(R_2=30\Omega\)
Tìm: \(R_{tđ}=?\)
Giải:
R1 R2 A B
Điện trở tương đương của mạch:
\(R_{tđ}=R_1+R_2=20+30=50\left(\Omega\right)\)
Đáp số: \(R_{tđ}=50\Omega\)

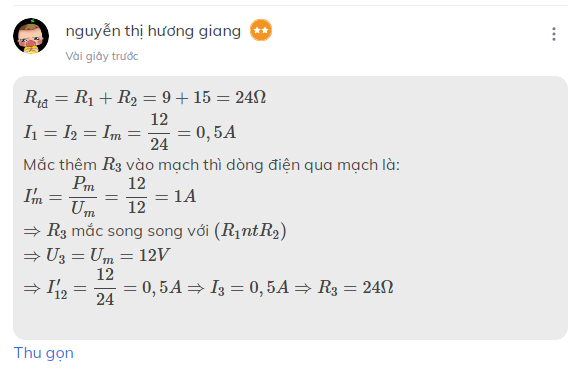
\(R_{tđ}=R_1+R_2=9+15=24\Omega\)
\(I_1=I_2=I_m=\dfrac{12}{24}=0,5A\)
Mắc thêm \(R_3\) vào mạch thì dòng điện qua mạch là:
\(I'_m=\dfrac{P_m}{U_m}=\dfrac{12}{12}=1A\)
\(\Rightarrow R_3\) mắc song song với \(\left(R_1ntR_2\right)\)
\(\Rightarrow U_3=U_m=12V\)
\(\Rightarrow I_{12}'=\dfrac{12}{24}=0,5A\Rightarrow I_3=0,5A\Rightarrow R_3=24\Omega\)

a. \(R=R1+R2=40+60=100\left(\Omega\right)\)
b + c. \(I=I1=I2=2,2A\left(R1ntR2\right)\)
\(\left[{}\begin{matrix}U=IR=2,2.100=220\left(V\right)\\U1=I1.R1=2,2.40=88\left(V\right)\\U2=I2.R2=2,2.60=132\left(V\right)\end{matrix}\right.\)
MCD R1 nt R2
a,Điện trở tương đương của đoạn mạch
\(R_{tđ}=R_1+R_2=40+60=100\left(\Omega\right)\)
b,Hiệu điện thế giữa 2 đầu đoạn mạch
\(U=R\cdot I=100\cdot2,2=220\left(V\right)\)
c,Hiệu điện thế giữa 2 đầu mỗi điện trở
\(I_1=I_2=I=2,2\left(A\right)\)
\(U_1=R_1I_1=40\cdot2,2=88\left(V\right)\)
\(U_2=I_2R_2=2,2\cdot60=132\left(V\right)\)

Bài 3 ) R1ntR2=>Rtđ= R1+R2=30 ohm
Bài 4 R1ntR2=>RTđ=120 ohm =>I1=I2=I=\(\dfrac{U}{Rtđ}=0,1A\)
Bài 5) R1ntR2ntR3=>RTđ=R1+R2+R3=50 ohm
=>I1=I2=I3=I=\(\dfrac{U}{Rtđ}=0,24A\)
Bài 6 )Ta có Rtđ=R1+R2=5+2R2 => I1=I2=I=\(\dfrac{30}{5+R2}=\dfrac{20}{R2}=>R2=10\Omega\)
Bài 7 ) a) Rtđ=R1+R2+R3=50 ohm
b) I1=I2=I3=I=\(\dfrac{75}{50}=1,5A\)
c) U1=I1.R1=15V
U2=I2.R2=22,5V
U3=I3.R3=37,5V
Vậy.........

Công thức tính điện trở tương đương đối với:
Đoạn mạch gồm hai điện trở R1 và R2 mắc nối tiếp: Rtđ = R1 + R2
Đoạn mạch gồm hai điện trở R1 và R2 mắc song song.
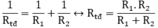

Điện trở tương đương của đoạn mạch là:
\(R_{tđ}=R_1+R_2+R_3=20+30+60=110\left(\Omega\right)\)
\(R_{tđ}=R_1+R_2=13+52=65\left(\Omega\right)\)