Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn sử dụng đường tb vủa hình thang ý
tao sẽ có công thức ZK=\(\dfrac{TV+RS}{2}\) =>2ZK=TV+RS(DPCM)

Câu 1:
a: Xét ΔJOH vuông tại O và ΔING vuông tại N có
JH=IG
\(\widehat{JHO}=\widehat{IGN}\)
Do đó: ΔJOH=ΔING
SUy ra: HO=NG
=>HN=GO
b: Xét ΔIJH và ΔJIG có
JI chung
JH=IG
IH=JG
Do đó: ΔIJH=ΔJIG
Suy ra: \(\widehat{PIJ}=\widehat{PJI}\)
=>ΔPJI cân tại P
=>PI=PJ
Ta có PJ+PG=JG
PI+HP=IH
mà JG=IH
và PI=PJ
nên PG=PH

1)Xét tam giác PSQ có PD=DS(gt),PA=AQ(gt)
=>DA là đường trung bình của tam giác PSQ
=>DA//SQ,DA=1/2SQ(1)
Xét tam giác RSQ có RC=CS(gt),RB=BQ(gt)
=>CB là đường trung bình của tam giác RSQ
=>CB//SQ,CB=1/2SQ(2)
Từ (1) và (2)=> DA//CB,DA=CB
=>ABCD là hình bình hành(3)
Xét tam giác SPR coSD=DP(gt),SC=CR(gt)
=>DC là đường trung bình của tam giác SPR
=>DC//PR
Ta có PR vuông góc với SQ(gt)
Mà SQ//DA(cmt)
=>PR vuông góc với DA
Mặt khác DC//PR(cmt)
=>DC vuông góc với DA hay góc ADC=90(4)
Từ (3) và (4)=>ABCD là hình chứ nhật
2)
Xét tam giác BAC có BU=UA(gt), BV=VC(gt)
=>UV là đường trung bình của tam giác BAC
=>UV//AC, UV=1/2AC (1)
Xét tam giác DAC có DZ=ZA(gt),DT=TC(gt)
=>ZT là đường trung bình của tam giác DAC
=>ZT//AC, ZT=1/2AC (2)
Từ (1) và (2) => UV//ZT, UV=ZT
=>UVTZ là hình bình hành(3)
Xét tam giác ABD có AZ=ZD(gt),AU=UB(gt)
=>UZ là đường trung bình của tam giác ABD
=>UZ//BD, UZ=1/2BD
Ta có BD vuông góc với AC(gt)
Mà UV//AC
=>BD vuông góc với UV
Mà UZ//BD(cmt)
=> UZ vuông góc với UV hay góc VUZ=90(4)
Từ (3) và (4)=> UVTZ là hình chữ nhật(5)
Mặt khác UV=1/2AC(cmt), UZ=1/2BD
Mà AC=BD
=>UV=UZ(6)
Từ (5) và (6)=>UVTZ là hình vuông
 Nga Phạm
Nga Phạm

Xét ΔPQS có PA/PQ=PD/PS
nên AD//QS và AD=1/2QS
Xét ΔRQS có RB/RQ=RC/RS
nên BC//QS và BC=1/2QS
=>AD//BC và AD=BC
Xét ΔQPR có QA/QP=QB/QR
nên AB//PR
=>AB vuông góc với QS
=>AB vuông góc với AD
=>ABCD là hình chữ nhật

xét tam giác MEN và tam giác PGN co :
ME=PG( giả thiết)
góc MEN=goc PGN (=90 độ)
EN=NG(GIẢ THIẾT)
DO đó tam giác MEN =tam giác PGN (c.g.c)
suy ra MN=PN(hai cạnh tương ứng) 1
Ta được :
PN=QP(2)
PQ=QM(3)
QM=MN(4)
Từ (1) (2) (3) (4) suy ra MN=PN=QP=MQ
Vậy MNPQ là hình thoi
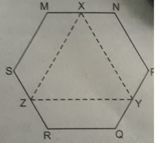
T V R S Z K
Trong sách nó vẽ dài dòng qua mình rút gọn lại .
Lời giải ...........................
Ta có :
\(TV\) // \(RS\)
\(TZ=ZR\) và \(VK=KS\)
\(\Rightarrow ZK=\dfrac{1}{2}\left(TV+RS\right)\)
\(\Rightarrow TV+RS=ZK:\dfrac{1}{2}\)
\(\Rightarrow TV+RS=2ZK\left(đpcm\right)\)
Kẻ ZY // TV (Y thuộc RV )
- Xét tam giác RTV CÓ :
ZY // TV
Z là trung điểm TR
Suy ra Y là trung điểm RV
Suy ra 2ZY = TV (*)
- Xét tam giác VRS có :
Y là trung điểm RV
K là trung điểm VS
Suy ra YK // RS
Suy ra 2YK = RS (**)
- Vì ZY // RS và YK // RS
Suy ra Z , Y , K thẳng hàng
Suy ra ZY + YK = ZK (***)
Từ (*) , (**) , (***)
Suy ra TV + RS = 2ZY + 2YK = 2(ZY +YK ) = 2ZK