Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M Q N P I
gọi I là giao điểm của QM và BD
Áp dụng định lí Mê-nê-la-uyt cho \(\Delta ABD\)
\(\frac{AQ}{QD}.\frac{ID}{IB}.\frac{MB}{MA}=1\)
vì Q,M,I thẳng hàng , kết hợp với MA = QA suy ra \(\frac{MB}{QD}.\frac{ID}{IB}=1\)
Ta có : MB = NB ; DP = DQ ; PC = NC
nên \(\frac{NB}{DP}.\frac{ID}{IB}=1\Rightarrow\frac{PC}{PD}.\frac{ID}{IB}.\frac{NB}{NC}=1\)
do đó , theo định lí Mê-nê-la-uyt thì I,N,P thẳng hàng
từ đó ta được đpcm

Ai tk mình đi mình bị âm nè mình hứa sẽ k lại!
Cảm ơn trc nha

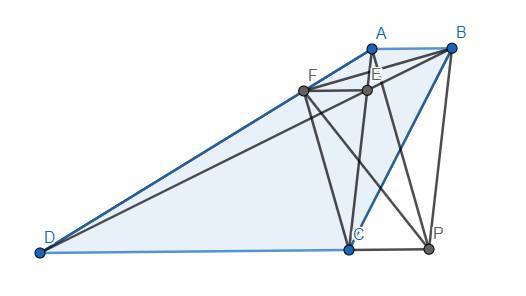
Dựng hình bình hành ABPC. Khi đó \(AD=AB+CD=CP+CD=DP\)
Ta có \(\dfrac{AB}{FE}=\dfrac{DA}{DF}\), \(\dfrac{CD}{FE}=\dfrac{DA}{AF}\)
\(\Rightarrow\dfrac{AB+CD}{FE}=DA\left(\dfrac{1}{DF}+\dfrac{1}{AF}\right)\)
\(\Rightarrow\dfrac{1}{FE}=\dfrac{DA}{DF.AF}\) \(\Rightarrow\dfrac{DF}{FE}=\dfrac{DP}{FA}\) \(\Rightarrow\dfrac{DF}{DC}=\dfrac{DP}{DA}=1\)
Từ đó \(\Delta DFC\) cân tại D. \(\Rightarrow\widehat{DFC}=\widehat{DCF}=\widehat{CFE}\) \(\Rightarrow\) FC là tia phân giác của \(\widehat{DFE}\). CMTT, FB là tia phân giác của \(\widehat{AFE}\). Do đó \(\widehat{BFC}=90^o\) (đpcm)

Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
tick nha