Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) ta có : \(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NB}+\overrightarrow{DM}+\overrightarrow{MN}+\overrightarrow{NC}\)
\(=2\overrightarrow{MN}+\left(\overrightarrow{AM}+\overrightarrow{DM}\right)+\left(\overrightarrow{NB}+\overrightarrow{NC}\right)=2\overrightarrow{MN}\left(đpcm\right)\)
b) ta có : \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AI}+\overrightarrow{IJ}+\overrightarrow{JB}+\overrightarrow{CI}+\overrightarrow{IJ}+\overrightarrow{JD}\)
\(=2\overrightarrow{IJ}+\left(\overrightarrow{AI}+\overrightarrow{CI}\right)+\left(\overrightarrow{JB}+\overrightarrow{JD}\right)=2\overrightarrow{IJ}\left(đpcm\right)\)
bn dùng định lí ta lét chứng minh được \(\overrightarrow{MJ}=\overrightarrow{IN}=\dfrac{1}{2}\overrightarrow{AB}\)
C) ta có : \(\overrightarrow{MN}+\overrightarrow{IJ}=\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BN}+\overrightarrow{IA}+\overrightarrow{AB}+\overrightarrow{BJ}\)
\(=2\overrightarrow{AB}+\left(\overrightarrow{MA}+\overrightarrow{BJ}\right)+\left(\overrightarrow{BN}+\overrightarrow{IA}\right)\)
\(=2\overrightarrow{AB}+\left(\overrightarrow{DM}+\overrightarrow{JD}\right)+\left(\overrightarrow{NC}+\overrightarrow{CI}\right)=2\overrightarrow{AB}+\overrightarrow{JM}+\overrightarrow{NI}\) \(=2\overrightarrow{AB}+\overrightarrow{BA}=\overrightarrow{AB}\left(đpcm\right)\)d) ta có : \(\overrightarrow{IM}+\overrightarrow{IN}=\overrightarrow{IJ}+\overrightarrow{JM}+\overrightarrow{IN}=\overrightarrow{IJ}\left(đpcm\right)\)
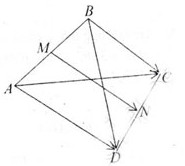
N là trung điểm của CD:
2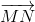
=
+ 
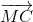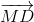(1)
Theo quy tắc 3 điểm, ta có:
= 
+
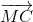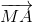(2)
= 
+ 
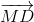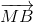(3)
Từ (1), (2), (3) ta có: 2= +++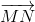
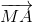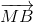
vì M là trung điểm của Ab nên: + =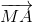 
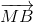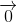
Suy ra : 2 = +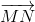
Chứng minh tương tự, ta có 2 =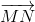 
+
Chú ý: Sau khi chứng minh 2 C = + ta chỉ cần chứng minh thêm + = + cũng được
Ta có: + = 
++
+
= +++= ++
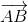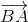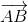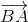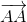
Vì 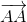= 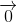nên ta có: +=+
và 2= + = +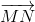
\(\left|\overrightarrow{MA}+\overrightarrow{MC}-\overrightarrow{MN}\right|=\left|\overrightarrow{MA}+\overrightarrow{MD}+\overrightarrow{DC}-\overrightarrow{MN}\right|\)\(=\left|\overrightarrow{DC}-\frac{1}{2}\overrightarrow{DC}-\frac{1}{2}\overrightarrow{AB}\right|=\left|\overrightarrow{DC}-\frac{3}{4}\overrightarrow{DC}\right|=\frac{1}{A}DC=\frac{a}{2}\)