Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có tam giác ADH vuông tại H
=> AH^2+HD^2=AD^2
=>HD^2=AD^2-AH^2
=5^2-4^2
=9
=>HD=3 cm
kẻ BK vuông góc với CD
=>ABKH là hình chữ nhật
=>AH=BK=4cm
tam giác BKC vuông tại K
=>BK^2+KC^2=BC^2
=>KC^2=BC^2-BK^2
=80-16
=64
=>KC=8 (cm)
lại có DH+HK+KC=20
=>HK=20-3-8=9 (cm)
=>AB+HK=9 cm
ta có chu vi hình thang ABCD là AB+BC+CD+DA=9+√80+20+5=34+√80(cm)

a) Chứng minh
DADH = DBCK (ch-gnh)
Þ DH = CK
Vận dụng nhận xét hình thang ABKH (AB//KH) có AH//BK Þ AB = HK
b) Vậy D H = C D − A B 2
c) DH = 4cm, AH = 3cm; SABCD = 30cm2
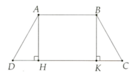

a) Xét ΔADH vuông tại H và ΔBCK vuông tại K có
AD=BC(ABCD là hình thang cân)
\(\widehat{D}=\widehat{C}\)(ABCD là hình thang cân)
Do đó: ΔADH=ΔBCK(cạnh huyền-góc nhọn)
Suy ra: DH=CK(hai cạnh tương ứng)

a) \(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{10+6}{2}.5=40\left(cm^2\right)\)
b) Xem hình vẽ
A B C D E 6 4 5 F
Tam giác vuông EAD có: \(AE=\sqrt{AD^2-DE^2}=\sqrt{5^2-4^2}=3\)
Vì ABCD là hình thang cân nên AE = FB = 3.
Suy ra AB = EF + AE + FB = 6 + 3 + 3 = 12.
\(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{12+6}{2}.4=36\left(cm^2\right)\)
