Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/C/m: BEDF là hbh
2/C/m: Dùng tính chất đường trung bình chứng minh M là t/d AN và N là t/d MC.
3/C/m: ME là đường trung bình tam giác ANB và NF là đường trung bình tam giác MDC
4/C/m: EMFN là hbh ( t/g có 2 cạnh đối vừa song vừa bằng nhau)

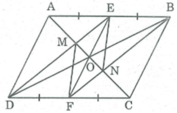
Xét ∆ EOM và ∆ FON có: ∠ (MEO) = ∠ (NFO) (so le trong do DE//BF)
OE = OF (tính chất hình bình hành)
∠ (MOE)= ∠ (NOF) (đối đỉnh )
Suy ra: ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).

a, Ta có:ABCD la hình bình hành=>AB=CD;AB//CD
mà E là trung diểm của AB;Flà trung điểm của CD
=>AE=EB=CF=DF(1)
VÌ AB//CD=>EB//DF(2)
Từ(1) và (2)=> EBFD là hình bình hành( theo dấu hiệu nhận biết hình bình hành)(đpcm)
b, Xét hbh ABCD có
AC cắt BD tại trung diểm củaAC và BD(1)
Xét hbh EBFD có EF cắt BD tại trung điểm của EF và BD(2)
từ (1) và (2)=>ba dường thang AC,BD,EF đồng quy
c,GỌI GIAO DIỂM CỦA AC,BD,EF LÀ O
Xét tam giác EOM và tam giác NOF có
góc EOM=góc NOF( đói đỉnh)
OE=OF(vi O là trung điểm cua EF)
goc MEF=góc NFE(vì CE//BF)
=>TAM GIAC EOM=TAMGIAC NOF
=.ME=NF(1)
TA CÓ ME//FN(2)
TU (1) VA(2)=>ENFM LA HBH

a) Xét Tứ giác DEBF ta có:
EB // DF ( vì AB // CD )
EB = DF ( vì = \(\frac{1}{2}\) AB và DC ( AB =DC) ) [ nếu không đúng cách trình bày thì bạn có thể sửa lại câu từ cho hay]
\(\Rightarrow\)tứ giác DEBF là hbh

a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
b: ta có: DEBF là hình bình hành
nên Hai đường chéo DB và EF cắt nhau tại trung điểm của mỗi đường(1)
Ta có:ABCD là hình bình hành
nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra BD,EF,AC đồng quy