Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S A B C D I K M N P O H L
a/
Gọi O là giao của AC và BD
Trong mp (SAC) Nối PN \(\Rightarrow PN\in\left(SAC\right)\) (1)
Trong mp (BDI) Nối OI có
\(O\in AC;AC\in\left(SAC\right)\Rightarrow O\in\left(SAC\right)\)
\(I\in SC;SC\in\left(SAC\right)\Rightarrow I\in\left(SAC\right)\)
\(\Rightarrow OI\in\left(SAC\right)\)(2)
Ta có
\(O\in BD;BD\in\left(BDI\right)\Rightarrow O\in\left(BDI\right);I\in\left(BDI\right)\Rightarrow OI\in\left(BDI\right)\)
Từ (1) và (2) => PN cắt OI gọi K là giao của PN với OI
Ta có
\(K\in PN\)
\(K\in OI;OI\in\left(BDI\right)\Rightarrow K\in\left(BDI\right)\)
=> K là giao của PN với (BDI)
b/
\(PM\in\left(SAB\right);PM\in\left(CMP\right)\) => PM là giao tuyến của (SAB) với (CMP) (1)
\(CM\in\left(SBC\right);CM\in\left(CMP\right)\) => CM là giao tuyến của (SBC) với (CMP) (2)
Ta có
\(S\in\left(SAC\right);S\in\left(SBD\right)\) và \(O\in\left(SAC\right);O\in\left(SBD\right)\) => SO là giao tuyến của (SAC) và (SBD)
Trong mp (SAC) nối CP => CP cắt SO tại H
Ta có \(H\in SO;SO\in\left(SBD\right)\Rightarrow H\in\left(SBD\right)\)
Trong mp (SBD) nối MH cắt SD tại L
Ta có
\(MH\in\left(CMP\right);L\in MH\Rightarrow L\in\left(CMP\right)\Rightarrow PL\in\left(CMP\right);PL\in\left(SAD\right)\) => PL là giao tuyến (SAD) với (CMP) (3)
Ta có \(CL\in\left(CMP\right);CL\in\left(SCD\right)\) => CL là giao tuyến của (SCD) với (CMP) (4)
Từ (1) (2) (3) (4) => thiết diện của S.ABCD với (CMP) là tứ giác CMPL

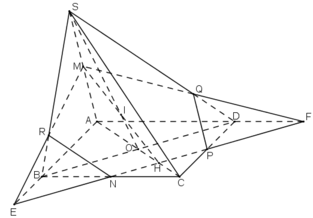
a) Tìm thiết diện :
Trong mp(ABCD), gọi F = AD ∩ PN và E = AB ∩ PN
Trong mp(SAD), gọi Q = MF ∩ SD
Trong mp(SAB), gọi R = ME ∩ SB
Nối PQ, NR ta được các đoạn giao tuyến của mp(MNP) với các mặt bên và mặt đáy của hình chóp là MQ, QP, PN, NR, RM
Vậy thiết diện cắt bởi mặt phẳng (MNP) là ngũ giác MQPNR.
b) Tìm SO ∩ (MNP). Gọi H là giao điểm của AC và PN .
Trong (SAC), SO ∩ MH = I
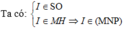
Vậy I = SO ∩ (MNP).

a) (SAD) ∩ (SBC) = SE
b) Trong (SBE): MN ∩ SE = F
Trong (SAE): AF ∩ SD = P là điểm cần tìm
c) Thiết diện là tứ giác AMNP
TenAnh1 A = (-0.14, -7.4) A = (-0.14, -7.4) A = (-0.14, -7.4) B = (14.46, -7.36) B = (14.46, -7.36) B = (14.46, -7.36) C = (-3.74, -5.6) C = (-3.74, -5.6) C = (-3.74, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) D = (11.62, -5.6)

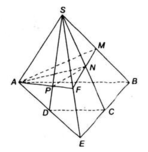
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
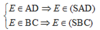
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.

a, Mình nghĩ ý bạn là (MNP)
Trong (ABCD) gọi E = \(NP\cap BD\)
⇒ E ∈ (SBD)
Do K ∈ SD ⇒ K ∈ (SBD). M là trung điểm của SB ⇒ M ∈ (SBD)
Trong (SBD) gọi F = BK \(\cap\) ME
⇒ \(\left\{{}\begin{matrix}F\in BK\\F\in\left(MNP\right)\end{matrix}\right.\) ⇒ F = BK \(\cap\) (MNP)
b, Trong (ABCD) gọi O = AC \(\cap\) BD và H = BN \(\cap\) AC
Trong (SBD) gọi G = BK \(\cap\) SO
Trong (SAC) gọi I = SA \(\cap\) HG
(BNK) \(\cap\) (SAD) = IK
(BNK) \(\cap\) (SCD) = KN
(BNK) \(\cap\) (ABCD) = NB
(BNK) \(\cap\) (SAD) = BI
⇒ Thiết diện tạo bởi hình chóp S.ABCD và (BNK) là tứ giác IKNB
s A B C D N P I o M
+ Chọn mp (SAC) chứa PN .
Ta có: - (SAC) giao ( BID) = I .
* I ∈ SC ⊂ (SAC).
* I ∈ ( BID).
Trong mp ( ABCD) có : AC cắt BD tại O .
=> Giao tuyến là OI.
Cho OI cắt PN tại đâu thì đấy là giao điểm.