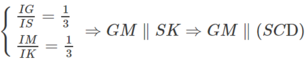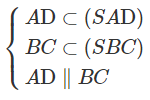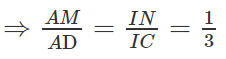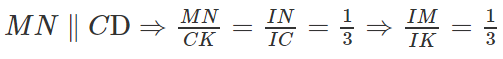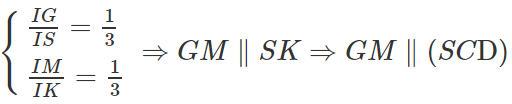Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn coi lại đề bài.
N,M,P,Q là các điểm trên CD, AD, SA hay trung điểm?
Vì nếu trung điểm thì làm sao thỏa mãn MD=2MC hay NA=3ND được?

a: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right);O\in BD\subset\left(SBD\right)\)
=>\(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
b: Xét (SAD) và (SBC) có
AD//BC
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
d: Trong mp(SAB), gọi I là giao điểm của AB với SM
\(I\in SM;I\in AB\subset\left(ABCD\right)\)
Do đó: I là giao điểm của SM với mp(ABCD)

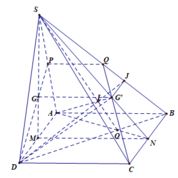
S A B C D E F G H M N P Q
Xét tg SNP có
\(\dfrac{SG}{GP}=\dfrac{SF}{FN}=2\) => GF//NP (Talet đảo trong tg)
Mà \(NP\in\left(ABCD\right)\) => GF//(ABCD)
C/m tương tự ta cũng có
EF//(ABCD); GH//(ABCD); HE//(ABCD)

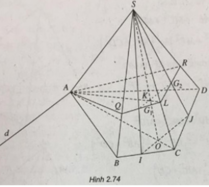
Gọi I, J lần lượt là trung điểm của BC, CD.
Ta có I J / / G 1 G 2 nên giao tuyến của hai mặt phẳng ( A G 1 G 2 ) và (ABCD) là đường thẳng d qua A và song song với IJ
Gọi O = IJ ∩ AC, K = G 1 G 2 ∩ S O , L = AK ∩ SC
L G 2 cắt SD tại R
L G 2 cắt SB tại Q
Ta có thiết diện là tứ giác AQLR.

a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
Mà 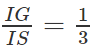
(G là trọng tâm của ∆SAB) nên
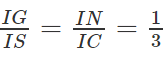
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
Ta có:

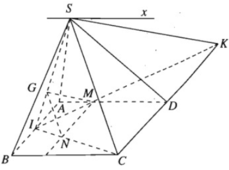
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
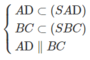
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
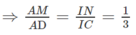
Mà 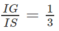
(G là trọng tâm của ∆SAB) nên
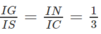 ⇒ GN // SC
⇒ GN // SC
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
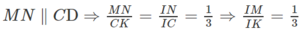
Ta có: