Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
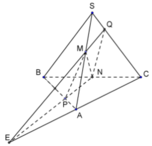
Trong mặt phẳng (ABC), gọi E = NP ∩ AC
Khi đó Q chính là giao điểm của SC với EM
Áp dụng định lý Menelaus vào tam giác ABC ta có:
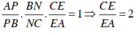
Áp dụng định lý Menelaus vào tam giác SAC ta có:
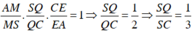


Gọi \(J=IP\cap SC\), ta có \(J=SC\cap\left(MNP\right)\)
Gọi \(E=NP\cap CD\), ta có \(E=CD\cap\left(MNP\right)\)
Gọi \(K=JE\cap SD\), ta có \(K=SD\cap\left(MNP\right)\)

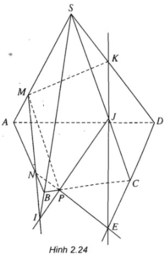
a lần lượt tìm giao điểm của mặt phẳng (MNP) với các đường thẳng chứa các cạnh của hình chóp.
Gọi I = MN ∩ SB
Ta có:
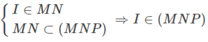
Vậy I = SB ∩ (MNP).
Từ đó, làm tương tự ta tìm được giao điểm của (MNP) với các cạnh còn lại.
Cụ thể :
Gọi J = IP ∩ SC, ta có J = SC ∩ (MNP)
Gọi E = NP ∩ CD, ta có E = CD ∩ (MNP)
Gọi K = JE ∩ SD, ta có K = SD ∩ (MNP)

a:
1: \(M\in SB\subset\left(SAB\right)\)
\(M\in\left(MNP\right)\)
Do đó: \(M\in\left(SAB\right)\cap\left(MNP\right)\)(1)
\(N\in AB\subset\left(SAB\right)\)
\(N\in\left(MNP\right)\)
Do đó: \(N\in\left(SAB\right)\cap\left(MNP\right)\left(2\right)\)
Từ (1),(2) suy ra \(\left(SAB\right)\cap\left(MNP\right)=MN\)
2:
\(M\in SB\subset\left(SBC\right);M\in\left(MNP\right)\)
=>\(M\in\left(SBC\right)\cap\left(MNP\right)\)(3)
\(P\in BC\subset\left(SBC\right);P\in\left(MNP\right)\)
=>\(P\in\left(SBC\right)\cap\left(MNP\right)\)(4)
Từ (3),(4) suy ra \(\left(SBC\right)\cap\left(MNP\right)=MP\)
3:
\(N\in AB\subset\left(ABC\right);N\in\left(MNP\right)\)
=>\(N\in\left(ABC\right)\cap\left(MNP\right)\)(5)
\(P\in BC\subset\left(ABC\right);P\in\left(MNP\right)\)
=>\(P\in\left(ABC\right)\cap\left(MNP\right)\left(6\right)\)
Từ (5),(6) suy ra \(\left(ABC\right)\cap\left(MNP\right)=NP\)
b: Xét ΔBAS có BN/BA=BM/BS
nên NM//AS
=>MN//(SAC)


Ta có M, N lần lượt là trung điểm của SA, SC
Do đó, tam giác SAC có MN // AC (1)
Ta có: \(\frac{{BP}}{{BA}} = \frac{{BQ}}{{BC}} = \frac{1}{3}\)
Suy ra: PQ // AC (2)
Từ (1) và (2), suy ra: MN // PQ
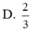
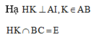


Thầy gợi ý cách xác định thiết diện thông qua hình vẽ sau:
Em kéo dài KN cắt AC tại P (trong mp(ABC)), từ đó tiếp tục dựng hình để xác định giao tuyến với các mặt còn lại của hình chóp để có thiết diện là tứ giác KMQN nhé